Filling shapes seems an easy task until you discover holes. In this extract from a chapter in my new book on JavaScript Graphics explains the hole theory and practice.

Now available as a paperback or ebook from Amazon.

JavaScript Bitmap Graphics
With Canvas

Contents

1. JavaScript Graphics
2. Getting Started With Canvas
3. Drawing Paths
     Extract: Basic Paths
     Extract: SVG Paths
     Extract: Bezier Curves
4. Stroke and Fill
     Extract: Stroke Properties 
     Extract: Fill and Holes
     Extract: Gradient & Pattern Fills
5. Transformations
     Extract: Transformations
     Extract: Custom Coordinates 
     Extract  Graphics State
6. Text
     Extract: Text, Typography & SVG 
     Extract: Unicode
7. Clipping, Compositing and Effects
     Extract: Clipping & Basic Compositing
8. Generating Bitmaps
     Extract:  Introduction To Bitmaps
     Extract :  Animation 
9. WebWorkers & OffscreenCanvas
     Extract: Web Workers
     Extract: OffscreenCanvas
   
10. Bit Manipulation In JavaScript
      Extract: Bit Manipulation
11. Typed Arrays
      Extract: Typed Arrays 
12. Files, blobs, URLs & Fetch
      Extract: Blobs & Files
      Extract: Read/Writing Local Files
      Extract: Fetch API **NEW!
13. Image Processing
      Extract: ImageData
      Extract:The Filter API
    
14. 3D WebGL
      Extract: WebGL 3D
15. 2D WebGL
    Extract: WebGL Convolutions

<ASIN:B07XJQDS4Z>

<ASIN:1871962579>

<ASIN:1871962560>

Paths are mathematical abstractions – lines of zero width and no color connecting mathematically exact points in a co-ordinate system. To convert a path into something physical it has to be rendered to the canvas bitmap. There are two way to do this, stroke and fill. The stroke function simply colors the outline of the path whereas the fill colors all of the points in the interior of the path. This all sounds easy and obvious, but in practice it is subtle and you need to understand it to get control of what exactly is happening.

In chapter but not in this extract:

• Color
• Stroke and Fill Color
• Stroke Properties
• Antialiasing

Fill, Stroke and the Painter’s Algorithm

You can combine a fill and a stroke and the effect that you get depends on the order that you perform them in. The basic principle is very simple - anything drawn after a given graphic will overwrite the graphic if they share pixels. This is generally called “the painter’s algorithm” because it is exactly what happens with physical paint – new paint covers up old paint. The way that new color is applied to pixels is in general more complicated than simply covering up the old, but this is the default behavior.

For example if you try:

var path1 = new Path2D();
path1.rect(50, 50, 200, 100);
ctx.lineWidth = 10;
ctx.strokeStyle = "black";
ctx.fillStyle = "lightgray";
ctx.fill(path1);
ctx.stroke(path1);

then what you will see is a gray rectangle with a 10-pixel outline as the rectangle is filled and then the outline is drawn over it. If you change the order of the fill and stroke functions then the result is a gray rectangle with a 5-pixel outline as the fill now covers the inner portion of the stroke.

Holes and Fill

A path can intersect with itself and in this case the question is how is the path filled? This can seem like a complicated question, but it is answered very simply. A point is either inside or outside of the path. If it is inside then it is part of the fill and if it is outside of the path it isn’t filled.

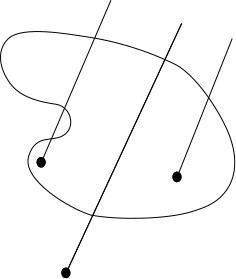
For simple connected paths, the question can be answered quite easily. If you pick a point and draw a line from it to infinity, a ray, if the line intersects with the path once the point is inside; if it intersects twice it is outside. More generally a point that has a ray that intersects an odd number of times is an interior point and if it intersects an even number of times it is an exterior point.

This is called the odd-even rule and you can use it to determine how paths are filled. For example, consider the star path made of two triangle sub-paths. Is the central area a hole or part of the interior? Using the odd-even rule you can see that the central area is an exterior region and should not be filled.

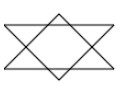
If you set the “evenodd” option in the fill then this is exactly what you see:

var Path1 = new Path2D();
Path1.moveTo(50, 50);
Path1.lineTo(100, 100);
Path1.lineTo(0, 100);
Path1.lineTo(50, 50);
Path1.moveTo(50, 110);
Path1.lineTo(0, 60);
Path1.lineTo(100, 60);
Path1.lineTo(50, 110);
ctx.stroke(Path1);
ctx.fill(Path1, "evenodd");

The odd-even rule is just one of the possible ways of defining the interior of a complex path. The non-zero winding rule is another, that also happens to be the default for the fill function. It works in the same way, but now we also take into account the direction that the path takes around a point.

The basic idea is that if the path winds around a point in the same direction then it is inside. The motivation comes from the physical intuition that if you surround a nail by a piece of string, representing the path, then if the nail is inside the path you cannot pull the string off the nail, but if it is outside the string is not “hung” on the nail. If you count a clockwise intersection with the path as +1 and an anticlockwise intersection with the path as -1 then the winding number is the sum of the values. For example in the example below the path intersects the ray once in the clockwise and once in the anticlockwise direction hence its winding number is zero and it is outside of the path.

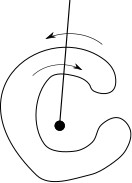
For connected curves a winding number of zero makes sense, but for disconnected curves things are slightly arbitrary. It is often believed that the non-zero rule fills in “holes” whereas the “odd-even” rule doesn’t. This isn’t exactly true.