| The Shape Of Classification Space Is Mostly Flat |
| Written by Mike James | |||
| Wednesday, 31 May 2017 | |||
|
All classification rules can be thought of as dividing up high dimensional spaces into areas that belong to different groups. Neural networks are no different, but until now we haven't had much insight into the shape of the dividing boundaries. The geometry is surprising.
A group of computer scientists, Alhussein Fawzi, Seyed-Mohsen Moosavi-Dezfooli, Pascal Frossard and Stefano Soatto from UCLA and EPFL have used Riemannian geometry to study the decision boundaries that are created when a deep neural network is trained. Many classifiers use relatively simple surfaces to attempt to separate different classes. For example, discriminant analysis and simple SVM divide the space using flat hyperplanes. To create curved division surfaces you have to include additional functions that introduce that curvature for example using polynomials or kernel functions. Deep neural networks are different in that in principle they can create complex curved boundaries using just the raw data. This is often supposed to be one of the reasons they are so powerful but so far no one has studied the nature of the decision surfaces. This is a particularly relevant question because of the existence of adversarial examples which are small modifications to correctly classified examples which are then incorrectly classified. The first question is do neural networks tend to create connected or disconnected areas in the classification space? This sounds like an easy question to answer - and it is in two and possibly three dimensions, but when the space has hundreds of dimensions you can't just look at it and see if an area is connected. To test for a connected region two points with the same classification are selected and an attempt is made to find a path between them that stays within the group. The trick is to select a wide enough range of points to test that the region is connected. In this case three types of pairs were tried - random pair in the group, random in the group and a point in the group obtained by adverserially perturbing a point not in the group and random in the group and a random point perturbed to be in the group. The startling result is: "In all three scenarios, a continuous path always exists between points sampled from the same classification region." This of course doesn't prove the the region is connected - there may be two points not tested are aren't in the same connected component - but the probability after testing 1000 pairs is quite low. "This result suggests that the classification regions created by deep neural networks are connected in R d : deep nets create single large regions containing all points of the same label. More than that, the path that was found using the proposed path finding approach approximately corresponds to a straight path." The second finding that most of the connecting paths are roughly straight lines is probably a refection of the fact that as the dimension increases the volume of a region becomes much larger than the surface. There is simply a lot of interior and not much boundary to get in the way.
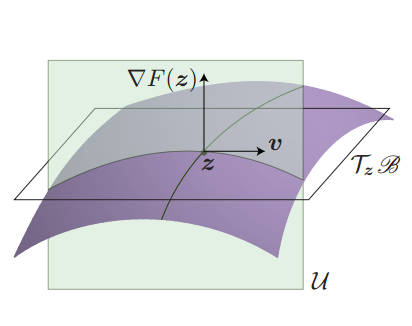
The normal curvature along a tangent vector v is the curvature of the intersection of the plane and the decision surface. Next the question of curvature was studied by computing the normal curvature and the set of directions that maximize it. The largest normal curvature is the principle curvature. A thousand random points were chosen and the perturbations computed to move the point to the decision boundary. At his point the principle curvature was computed. The result was a another surprise: "The decision boundary in the vicinity of natural images is flat in most directions, with only a very few directions that are significantly curved." Flat is now what most people would have expected. What is more when the boundary is curved the tendency is towards negative curvature and this seems to be a general property shared by different networks and datasets. These curved directions also seem to be shared by many data points. These observations can be used to detect adversarial images which do not follow the natural image tendency to negative curvature. The idea is to simply test to see if an image is in the region of a positively curved boundary - if so it is likely an adversarial image. The conclusion is a good summary: We analyzed in this paper the geometry induced by deep neural network classifiers in the input space. Specifically, we provided empirical evidence showing that classification regions are connected. Next, to analyze the complexity of the functions learned by deep networks, we provided a comprehensive empirical analysis of the curvature of the decision boundaries. We showed in particular that, in the vicinity of natural images, the decision boundaries learned by deep networks are flat along most (but not all) directions, and that some curved directions are shared across datapoints. We finally leveraged a fundamental observation on the asymmetry in the curvature of deep nets, and proposed an algorithm for detecting adversarially perturbed samples from original samples. This geometric approach was shown to be very effective, when the perturbations are sufficiently small, and that recovering the label was further possible using this algorithm. It seems that the geometry of the decision surfaces is more subtle than we thought. And "mostly flat" is an unexpected conclusion that means that the ability to use curved decision surfaces isn't the key property in making a deep neural network so effective. The difference between natural and adversarial images is a strange one and need more thought and investigation. It is also clear that thinking about high dimensional spaces is hard.
More InformationClassification regions of deep neural networks Related ArticlesAlphGo Defeats World's Top Ranking Go Player Evolution Is Better Than Backprop? A Single Perturbation Can Fool Deep Learning Artificial Intelligence - strong and weak
To be informed about new articles on I Programmer, sign up for our weekly newsletter, subscribe to the RSS feed and follow us on Twitter, Facebook or Linkedin.
Comments
or email your comment to: comments@i-programmer.info |
|||
| Last Updated ( Wednesday, 31 May 2017 ) |