| The McCulloch-Pitts Neuron |
| Written by Mike James | ||||
| Thursday, 04 March 2021 | ||||
Page 1 of 3 Nowadays the McCulloch-Pitts neuron tends to be overlooked in favour of simpler neuronal models, but it was, and still is, important. It proved that something that behaved like a biological neuron was capable of computation and influenced early computer designers.
Before the neural network algorithms in use today were devised, there was an alternative. It was invented in 1943 by neurophysiologist Warren McCulloch and logician Walter Pitts. Now networks of the McCulloch-Pitts type tend to be overlooked in favour of “gradient descent” type neural networks and this is a shame. McCulloch-Pitts neurons are more like the sort of approach we see today in neuromorphic chips where neurons are used as computational units.
Warren McCulloch
Walter Pitts What is interesting about the McCulloch-Pitts model of a neural network is that it can be used as the components of computer-like systems. In fact many early computers - Turings design for the ACE for example - were planned using McCulloch-Pitts style logic components. That is, where neural networks are commonly used to learn something, a McCulloch-Pitts neuron is constructed to do a particular job. OK, I have to admit that in many cases the same job can be done just as well using traditional Boolean components, but it is interesting to see how it all works using components which are closer to “biological” components. It gives you an idea, although probably not the whole idea, of how the brain might just be a computer. The Biological NeuronThe basic idea of a McCulloch-Pitts model is to use components which have some of the characteristics of real neurons.
Image Credit: Quasar Jarosz
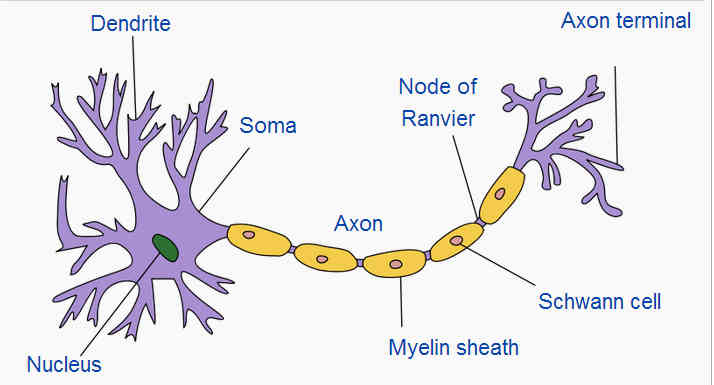
A real neuron has a number of inputs, the dendrites, which are “excitatory” and some which are “inhibitory”. What the neuron does depends on the sum of inputs. The excitatory inputs tend to make the cell fire and the inhibitory inputs make is not fire – i.e. pass on the signal. When the cell fires a signal propagates down the axon which acts like the output wire and then is applied to the inputs of other neurons via the axon terminals. You can think of it as a sort of battle to control the neuron with the excitatory inputs pushing it to fire and the inhibitory inputs stopping it. There are lots of complications to this basic model – in particular a neuron fires a train of pulses rather than just changing its state - but the idea of inhibitory fighting excitatory seems to be the key behaviour. How can we create an easier to use model of the neuron? A Simple ModelWhat we need is a model of the neuron that doesn't capture all of its properties and behaviour but just enough to capture the way it performs compuation. So what we have to do is throw away aspects of the way the cell behaves in an effort to simplify without destroying its action. First let’s just have a cell that gives out a binary state – zero or one, on or off. The inputs then carry a binary signal and the only thing that matters is the number of “on” signals on the excitatory versus the inhibitory inputs. We have essentially a “threshold” gate model of the neuron. This turns out to be a bit too complicated to analyse so we make one more big simplification – the inhibitory input overrides the excitatory. That is, if an inhibitory input is on the cell cannot fire (i.e. it is off) no matter what the excitatory inputs are doing. With this small change things are made a lot easier and we can now define precisely what a McCulloch-Pitts neuron is:
The rule for its operation is that at time t it looks at its excitatory inputs and counts up the number of ones present. If the count is equal to or greater than the threshold AND the inhibitory input is zero then at time t+1 the cell outputs a one, otherwise it outputs a zero. Notice that this rule is more complicated than you might think at first and it does give rise to behaviours that are quite complicated. The key factor that you might just overlook is that we are using sequential logic that involves time. A clock is used to synchronise all of the cells in a network and they change state at each clock pulse. This is necessary to stop infinite period oscillation in some types of circuit. Standard LogicI’m going to use the symbols and notation introduced by Marvin Minsky. Minsky uses a symbol that shows a cell as a circle with its threshold written in. It is very easy to invent equivalents of the standard Boolean gates. For example, it is very easy to work out how to make OR, AND and NOT.
The basic gates of Boolean logic as McCulloch-Pitts Neurons
You should be able to see that the truth tables for each of these cells is equivalent to the corresponding Boolean gate. For example, for the AND cell, one input at one doesn’t fire the cell but two and only two at one does fire the cell – i.e. an AND gate as promised. The OR gate fires if either or both of its inputs are one because its threshold is one. The only tricky one is the NOT gate and you can see here that a single inhibitory input (shown with a circle at the end) combined with a threshold of zero gives the desired result. When the inhibitor is off the threshold is equalled, i.e. zero excitatory inputs and the cell give out a one. If the inhibitor is on then the cell is obviously off – a NOT gate as promised. |
||||
| Last Updated ( Thursday, 04 March 2021 ) |