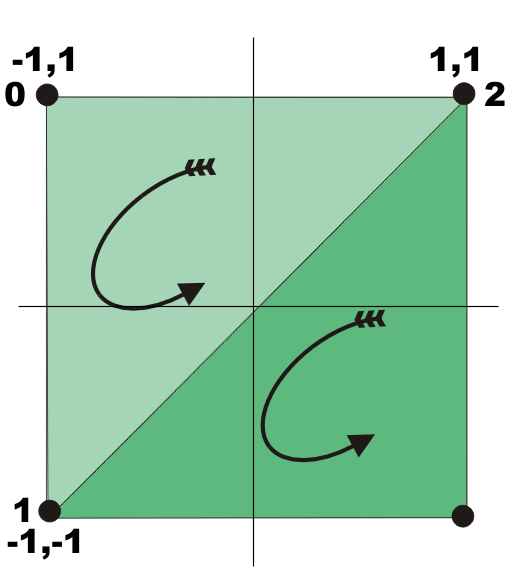
The first three vertexes, 0,1 and 2, correspond to the light green triangle:

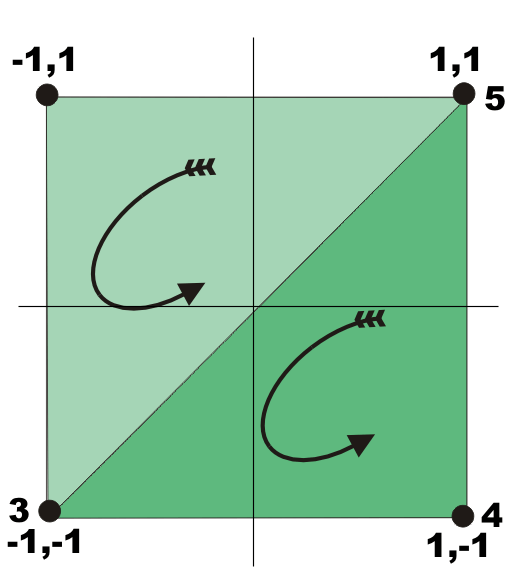
The second three vertexes, 3, 4 and 5, correspond the the dark green triangle:

With this we can now move on and create the front face.  Notice that all we have created so far is an array of vectors which give the location of the points that make up a flat face consisting of two triangles. We now have to use this basic geometry to create vertexes.

To do this we use the constructor which accepts the position of the vertex as a Vector3 as the first parameter, the normal to the surface as a Vector3 as the second parameter and a Vector2 given the texture co-ordinates of the point as the third parameter. 

By default the XNA co-ordinate system is such that positive x is to the right, positive y is up and positive z is out of the screen towards the viewer.

The front face is constructed by moving the points forward in the z direction i.e. out of the screen -i.e. we simply add (0,0,1) or Vector3.UnitZ to the location of each point. The normal for the front face is simply a vector pointing out of the screen so it is Vector3.UnitZ for each vertex:

//front face
for (int i = 0; i <= 2; i++)
{
 vertexes[i] = 
   new VertexPositionNormalTexture(
        face[i] + Vector3.UnitZ, 
              Vector3.UnitZ, Texcoords);
 vertexes[i+3] = 
   new VertexPositionNormalTexture(
        face[i + 3] + Vector3.UnitZ, 
              Vector3.UnitZ, Texcoords);
}

//Back face
for (int i = 0; i <= 2; i++)
{
 vertexes[i + 6] = 
    new VertexPositionNormalTexture(
         face[2 - i] - Vector3.UnitZ, 
             -Vector3.UnitZ, Texcoords);
 vertexes[i + 6 + 3] = 
    new VertexPositionNormalTexture(
         face[5 - i] - Vector3.UnitZ, 
             -Vector3.UnitZ, Texcoords);
}

These definitions might look complicated but all that is happening is that the front face is created by moving the face one unit forward in the z direction and the back face one unit back in the z direction.

The front face has its vertexes listed in an anticlockwise order but the back face needs them in reverse order because it presents its clockwise back face to us in its present position.

<ASIN:0470584467>

<ASIN:1430231262>

<ASIN:0123751039>

<ASIN:1584505370>

<ASIN:0672330067>

<ASIN:0672330229>