Understanding the way interest rates affect cashflow is the key to both savings and loans.This chapter of Financial Functions with a Spreadsheet explores the relationship between Present Value and Future Value.

 Financial Functions

 Buy from Amazon

Spreadsheets take the hard work out of calculations, but you still need to know how to do them. Financial Functions with a spreadsheet is all about understanding and reasoning, using a spreadsheet to do the actual calculation.

1. Understanding Percentages
   Percentages are something familiar to us all - but they present many pitfalls that need to be avoided.
   
   
2. Interest Simple and Compound
   We explore the idea of borrowing money for a specified rate of interest or earning interest on an investment. The ideas of Present and Future Value PV and FV are introduced. 
   
   
3. Effective Interest Rates
   We explore the idea of the `effective’ annual interest rate and then on to the Effective Interest Rate/Annual Percentage Rate, the much quoted EIR or APR.
   
   
4. Introduction to Cashflow - Savings Plans
   In the first of three chapters covering the way in which interest rate affects cashflow we explore savings - but first we introduce some general ideas that apply equally to annuities and repayment loans.
   
   
5. Cashflow Continued - Annuities
   We move on to annuities in the second of three chapters devoted to exploring the way in which interest rate affects 
   
   
6. Exploring Repayment Loans
   Repayment loans are the subject of the last of three chapters which look at the effects of regular cashflows.
   
   

7. Present and Future Values
   The principles of present and future value apply even if the cash flow is irregular. The calculations are just a matter of breaking down the cash flow calculations into simple steps.
   
   

8. Investment Analysis
   How is it possible to evaluate investments that generate irregular cashflows? We explore how NPV can be used to make investment decisions.
   
   

9. Advanced Investment Analysis IRR and MIRR
   The IRR is perhaps the most complicated of the measures of the value of an investment with an irregular cash flow. Understanding exactly what it means is a good step toward making correct use of it. 
   
   

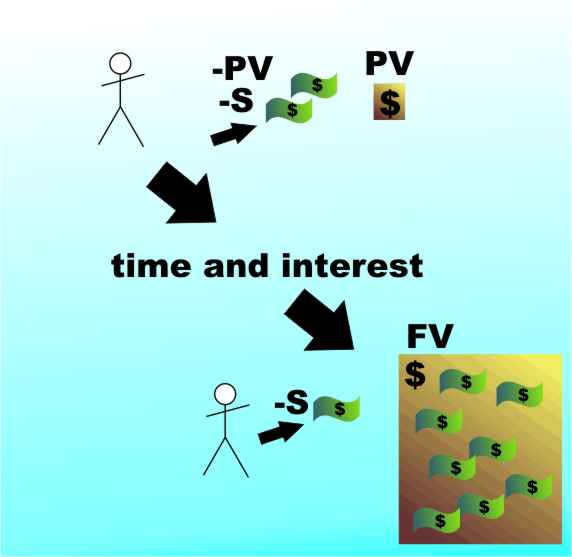
<ASIN:1871962013>

<ASIN:B07S79ZVMQ>

Chapter 4

This is the first of three chapters covering the way in which interest rate affects cashflow. In it we explore savings, but first we introduce some general ideas that apply equally to annuities and repayment loans which are covered in Chapters 5 and 6.

In the case of compound interest the value of the principal changes because of the interest added to it.

This is just the simplest case of a regular alteration of the principal at the end of each compounding period. The next step is to include a regular payment or withdrawl. 

This is a remarkably common situation encounted in three major financial transactions - repayment loans, savings plans and annuities.

Loans and annuities

In the case of a repayment loan or a mortgage (i.e. a repayment loan secured on property) the principal is reduced by the regular payment of the interest due plus an additional amount to pay off the loan. The repayments continue until the loan is paid off.

Repayment loans are commonly encountered as part of Hire Purchase agreements for all types of goods and as repayment mortgages.

Although repayment loans are the most common example of this type of transaction every loan situation has its corresponding incarnation as an investment. Seen from the other side of the table, as it were, a repayment loan is called an annuity.

In the case of an annuity a sum of money is placed on deposit and regular withdrawals composed of interest earned and capital are made. As in the case of a repayment loan the withdrawals continue until the deposit is reduced to zero.

Annuities are most commonly encountered as part of a pension provision but they are applicable in any situation where an asset has to be converted into a regular cashflow.

As well as the lender/borrower view point there is also another variation on the repayment loan/annuity situation. In both the repayment loan and annuity the flow of cash acts to reduce the principal.

In a regular savings plan the flow of cash acts to increase the principal. Apart from this change in direction of the cashflow the mathematics and many other consideration are identical.

Clearly the sorts of questions that interest us about repayment loans and annuities concern the size of the regular payment needed to reduce the principal to zero in a given number of years at the interest stated.

As you might guess the formulas are the same for repayment loans and for annuities.

PV and FV

The basic idea is that there is a sum of money at the start of the process - the Present Value (PV). This is increased by the action of interest over time and either increased of decreased by a regular payment to give a sum of money in the future - the Future Value FV.

We use the convention that the calculation is done from your point of view and money that you pay out is negative, i.e. it decreases your wealth.

In the case of a savings plan you initially deposit the present value (which is often zero) and make a regular payment each time period. As both of these are cashflows away from you, both are negative. Over time the action of interest and the regular payment increase the size of the deposit and hence its future value grows.

Notice that the FV is positive because it is money you own. 

 A savings plan - the deposit gets bigger due to the payments and the action of interest.

<ASIN:B07S79ZVMQ>