| Introduction to Cashflow |
Page 2 of 4
The situation with an annuity is very similar. In this case the deposit i.e the PV starts out big and gets smaller as you withdraw money from it. Interest still acts to increase the deposit but usually the effect of the withdrawl slowly reduces the deposit to its future value which is usually taken to be zero. In this case the cashflow in the first period is -PV representing the flow out of the present value and +S representing the payment flowing in. In most cases the FV, which is also positive in that it represents wealth you still hold, usually slowly decreases - however this isn't always the case.
An annuity - the principle value is decreased by payments but increased by interest.
Finally a repayment loan once again involves an initial sum only in this case the principle value is paid to you so it is positive and a regular payment from you, i.e. another negative cashflow slowly reduces the debt. Notice that the future value is negative as it represents a debt i.e. a negative asset.
A repayment loan - the principle is slowly eroded by a cashflow.
It has to be admitted that it is difficult to keep track of the signs of the cashflows but if you apply the principle that a cashflow out is negative and a cashflow in is positive it should all work out. Savings plansThe workings of a repayment loan or annuity are actually easier to understand if we first consider the closely related situation of a regular saving plan.
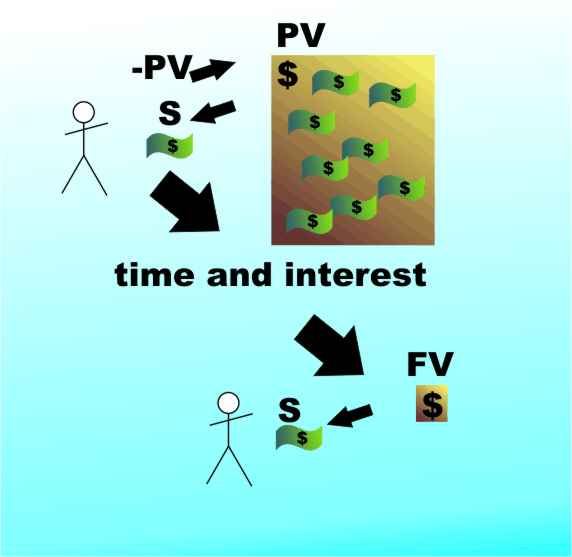
In this case a regular sum S (a payment usually denoted PMT) is deposited each period and the total sum accumulated attracts interest at I% (Rate) at the end of each period. It is a convention that the money is deposited at the end of each period and money that you pay out is negative. Thus after the first period the balance is simply the first regular payment:
After the second period the amount is the first regular payment plus the interest it has earned:
After the third period the amount is:
and so on. You can see that as each period passes the amount already on deposit is increased by being multiplied by (1+I) and has S added to it. To work out the Future Value of the savings plan after n periods you could simply construct a spreadsheet that calculates the repeated multiplication by (1+I) and adding S but there is a simpler way of working out the same thing. After a little math it can be shown that the Future Value is given by:
This is such a complicated looking formula that nearly all spreadsheets provide a single financial function, usually called FV, to calculate the same result. This is just the function we met in Chapter Two in the calculation of compound interest only now we can specify an initial deposit - the Present Value PV - and a regular payment S. FV functionThe common spreadsheet function:
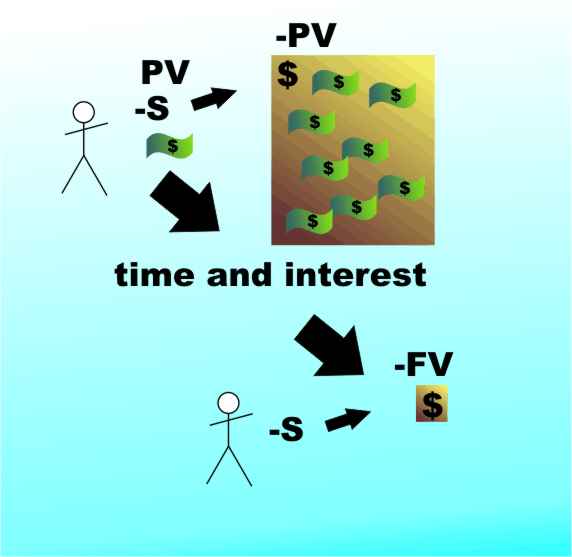
will calculate the Future Value FV of a regular saving of S, at I% for nper periods with a starting blance of PV which is often zero. If you don't specify the PV then it is assumed to be zero by default. Notice that as with nearly all financial functions it is best to regard the sums specified in the function, i.e. S and PV, as flowing from the depositor. So a deposit of $100 is -$100 and a payment of $10 per month into the account is -$10 per month. However the result of the function is the status of the account - postive when in credit and negative when in debt.
The cashflows are -PV and -S.
As with all financial calculations the interest rate has to be expressed in terms of the regular payment period and for a savings plan the money paid into the acount is negative. For example, if you start a savings plan that calls for $10 per month at 6% per annum paid monthly then after 5 years the Future Value will be
This is a horrible looking formulae and one that you are very likely to make mistakes in when trying to enter it into a spreadsheet. How much simpler the equivalent financial functions appears:
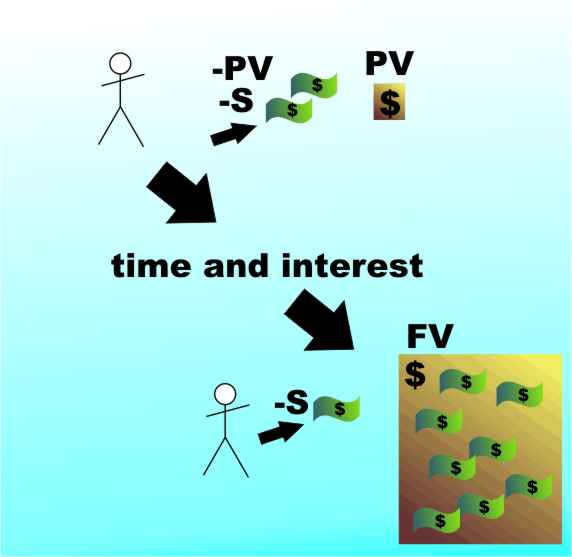
and this of course gives exactly the same result, $697.70. Notice that there is a minus sign in front of the payment - it is a convention that cash paid in (e.g. S) is negative while cash paid out (e.g. FV) is positive. If you make an initial deposit of PV at the start of the savings plan to get it going then the formula have to be altered to:
That is, the compounded interest earned by the initial deposit has to be added to the Future Value. In most spreadsheets you simply include the initial deposit as the optional Present Value (PV) parameter at the end of the previous formula.
For example, if deposit $100 and save $10 per month at 6% per annum paid monthly then after 5 years the Future Value will be:
which works out to $832.59 which is more than the previous result by $134.89 - the amount of interest earned by the initial $100 at 6% for 5 years. |