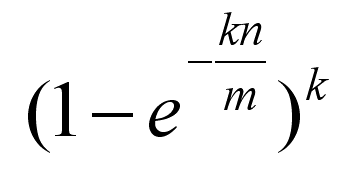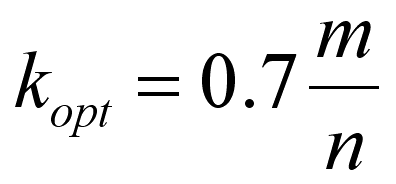| The Bloom Filter |
| Written by Mike James | |||||
| Thursday, 23 June 2022 | |||||
Page 1 of 2 You may never have heard of a Bloom Filter, but this ingenious algorithm is used in Google's BigTable database to avoid wasting time fruitlessly searching for data that isn't there. Killer Algorithms
Contents
* First Draft
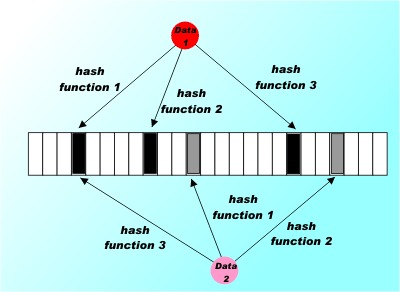
In programming, perhaps in life, there are certain well known trade-offs. You can usually trade space for time as in the more storage you can throw at a problem the faster you can make it run. There is also a lesser known trade-off which is much more sophisticated. In general, you can trade certainty for time. This the basis of many random algorithms where the solution returned isn't certain but it is fast compared to a deterministic calculation of the same quantity. These are ideas that fascinate many programmers who become completely absorbed by the study of algorithms for their own sake, but they also have practical application. Take for example the currently hot topic of the Bloom Filter. This might sound like something a creative photographer might put in front of his lens but it is in fact an intriguing algorithm that mixes trading both space and certainty for time. It can tell you if you have seen a particular data item before in ultra quick time - but it might be wrong! Bloom filters are used by Google's BigTable database to reduce lookups for data rows that haven't been stored. The Squid proxy server uses one to avoid looking up things that aren't in the cache and so on... Using hash functionsThe algorithm invented in 1970 by Burton Bloom is very simple but still ingenious. It relies on the use of a number of different hash functions. A hash function is a function that will take an item of data and process it to produce a value or key. For example, you could simply add up the code values for each character in a string and return the result mod some given value. A hash function always produces the same hash value from the same data but it is possible and in fact usual for two different data values to produce the same hash value. That is the hash value isn't unique to a given item of data and you can't reverse the hashing function to get the data values. The hash function is a many-one deterministic function. A good hash function also has other desirable properties such as spreading the hash values obtained as evenly as possible over the output range but for the moment let's just concentrate on the basic hash function. A Bloom filter starts off with a bit array Bloom[i] initialized to zero. To record a data value you simply compute k different hash functions and treat the resulting k values as indices into the array and set each of the k array elements to 1. You repeat this for every data item that you encounter.
In this case three hash functions are used to set three elements in the bit array for each data item. Notice that as illustrated these two data items both set the 4th element.
Now suppose a data item turns up and you want to know if you have seen it before. All you have to do is apply the k hash functions and look up the indicated array elements. If any of them are zero you can be 100% sure that you have never encountered the item before - if you had the bit would have been set to 1. However even if all of them are one then you can't conclude that you have seen the data item before because all of the bits could have been set by the k hash functions applied to multiple other data items. All you can conclude is that it is likely that you have encountered the data item before. Notice that it is impossible to remove an item from a Bloom filter. The reason is simply that you can't unset a bit that appears to belong to a data item because it might also be set by another data item. If the bit array is mostly empty i.e. set to zero and the k hash functions are independent of one another then the probability of a false positive i.e. concluding that we have seen a data item when we actually haven't is low. For example, if there are only k bits set you can conclude that the probability of a false positive is very close to zero as the only possibility of error is that you entered a data item that produced the same k hash values - which is unlikely as long as the hash functions are independent. As the bit array fills up the probability of a false positive slowly increases. Of course when the bit array is full every data item queried is identified as having been seen before. So clearly you can trade space for accuracy as well as for time. Interestingly a Bloom filter can also trade accuracy for space. If you think that to store an n byte string takes n bytes then in a Boom filter it only takes k bits and k comparisons but there is the possibility of false positives. As k is increased the storage needed increases along with the number of comparisons and the possibility of a false positive decreases. As with any trade-off situation that are optimal values. The approximate false positive (i.e. error) rate is:
where k is the number of hash functions, m is the size of the bit array and n is the number of items stored in the bit array. Using this you can work out the optimal k for given m and n, which is:
So for example, if the bit array has 1000 elements and you have already stored 10 data items then the optimum k is 70. You can also work out the size of the bit array to give any desired probability of error for a fixed n (assuming an optimum k):
So for example if you are storing 10 data items and you want the probability of a false positive to be around 0.001 you need an array with around 138 elements and a k around 10. A more realistic example, is when you are storing 100,000 items and need the probability of false positive to be around 0.000001 then you need an array that has around 350Kbytes of storage and k is around 20. |
|||||
| Last Updated ( Saturday, 25 June 2022 ) |