| Programmer's Guide To Theory - Numbers |
| Written by Mike James | ||||||
| Monday, 13 January 2020 | ||||||
Page 2 of 2
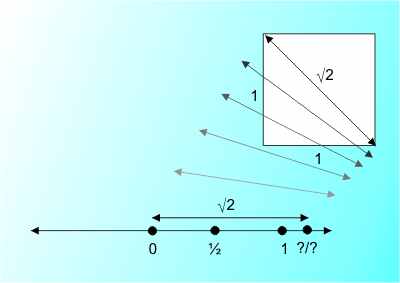
What this means is that if we only have the integers and the fractions or the rationals (because they are a ratio of two integers) then there are points on the line that do not correspond to a number - and this is unacceptable. The solution was that we simply expanded what we regard as a number and the irrational numbers were added to the mix. But what exactly are irrationals and how can you write one down? This is a question that occupied mathematicians for a long time and it took a while to get it right. Today we think of an irrational number as a value with an infinite sequence of digits after the decimal point. This sequence of digits goes on forever and can never fall into a repeating pattern because if it does it is fairly easy to show that the value is a rational. That is in decimal: 0.33333333333333 repeating for ever isn't an irrational number because it repeats and it is exactly 1/3 i.e. it is rational. Notice that there is already something strange going on because while we have an intellectual solution to what an irrational is, we still can't write one down. How could you as the digits never end and never fall into a repeating pattern. This means that in general writing an irrational down isn't going to be a practical proposition. And yet I can write down √2 and this seems to specify the number precisely. Also what sort of equations do irrationals solve? A partial answer is that they are solutions to equations like: xa=b Again a and b are rational with b positive and x is sometimes the new class of numbers i.e. an irrational. The problem is that only a relatively small proportion of the irrationals come from the roots of polynomials as we shall see. Now we have integers like 1 or -2, fractions like 5/6 and irrationals like √2. From the point of view of computing this is where it all gets very messy, but first we are now ready to look at the subtlety of infinity. The Number HierarchyThere is a standard mathematical procedure for defining and expanding the number system. Starting out with a set of numbers that are well defined, you look at simple equations involving those numbers. In each case you discover that some of the equations don't have a solution that is a number in the set of numbers you started with. To make these solutions available you add a new type of number to create a larger set of numbers. You repeat this until you end up with a set of numbers for which all the equations you can think up have a solution in the same set of numbers. That is, as far as equations go you now have a complete set of numbers. This sounds almost magical and the step that seems to hold the magic is when you add something to the existing set of numbers to expand its scope. It seems almost crazy that you can simply invent a new type of number. In fact it isn't magical because it is the equation that defines all of the properties of the new numbers. For example, you can't solve x2=2 using nothing but rational numbers. So you invent a symbol to represent the new number √2 and you can use it in calculations as if it was an ordinary number √2*2+3/4 and you simply work with the symbol as if it was a perfectly valid number. You can even occasionally remove the new symbol using the fact that √2*√2=2 which is, of course given by the equation that √2 solves. If you can get rid of all of the uses of the new symbol so much the better but if you can't then at the end of the calculation you replace the new symbol with a numeric approximation that gets you as close to the true answer as you need.
To summarize: In each case the equation listed is the one that leads to the next class of numbers, i.e. the one for which no solution exists in the current class of numbers. Notice that the complex numbers are complete in the sense that we don’t need to invent any more types of number to get the solutions of all equations that involve the complex numbers. The complex numbers are very important, but from our point of view we only need to understand the hierarchy up to the irrationals. Included in the chapter but not in this extract:
Summary
A Programmers Guide To Theory
Now available as a paperback and ebook from Amazon.
Contents
To be informed about new articles on I Programmer, sign up for our weekly newsletter, subscribe to the RSS feed and follow us on Twitter, Facebook or Linkedin.
Comments
or email your comment to: comments@i-programmer.info
|
||||||
| Last Updated ( Monday, 13 January 2020 ) |