| Fractal Image Compression |
| Written by Mike James | ||||||||||||||||||||||||
| Friday, 08 April 2022 | ||||||||||||||||||||||||
Page 4 of 5
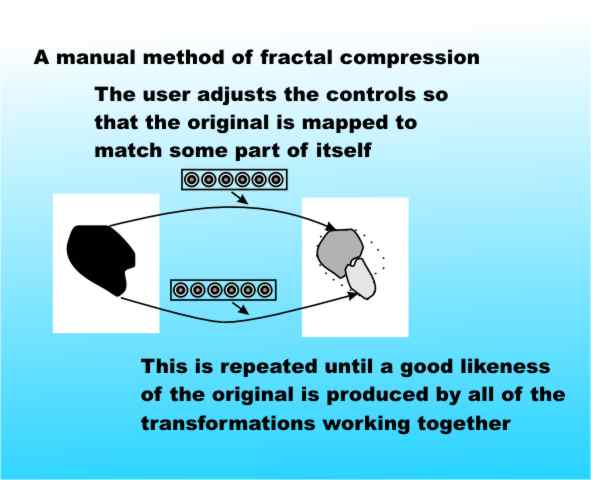
Smooth ChangesA secondary result that helps is the continuity condition. This says that as you alter the coefficients of the IFS the attractor changes smoothly and without any sudden jumps. This means that one method of performing the compression is to write a program which allows a user to manually fiddle with a set of controls in an effort to transform the original image into a passable likeness of itself under a set of contractive affine transformations. The resulting set of coefficients could then be used as the compressed version of the image.
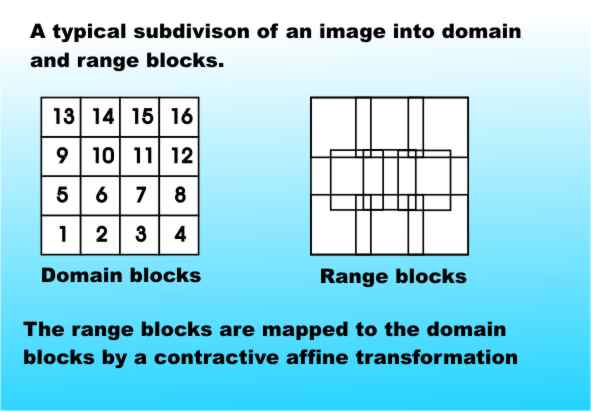
This is a workable method of compressing black and white images. As you add more transformations to the IFS then the accuracy of the representation increases - so you can trade storage for accuracy as in a traditional compression scheme. A practical schemeThe manual matching method of image compression does work but it is hardly a practical proposition if you want to compress hundreds of images. Fortunately there is a way to make the process automatic. The whole theory that we have been explaining still works if you consider contractive affine transformations that are restricted to work only on parts of the whole image. The idea is that instead of trying to find an affine transformation that maps the whole image onto part of itself you can try to find an affine transformation that maps one part of the image onto another part of the image. As most images have a high degree of affine redundancy - i.e. one part of the picture is near as makes no matter an affine copy of another - this should work well and perhaps even better than the manual method described earlier. In an ideal case the division of the image into parts would be done to optimise the matching of one part with another but such an intelligent approach would need a human to drive it. A fully automatic approach is only possible using a fixed division of the image into so called "domain" and "range" blocks. The range blocks contain parts of the image that will be mapped to the domain blocks in an attempt to match the original image. It is obvious that the domain blocks have to completely divide up the original image without overlap because we are interested in reconstructing the entire image. Also the range blocks have to overlap because they have to be bigger than the domain blocks - how else could the transformation from range to domain be contractive?
You can think of this as trying to find transformations that map big bits of the image into smaller bits of the image - but what transformations? The entire range of contractive affine transformations is a bit too big to handle so it is customary to restrict the attention to a smaller set. For example, you might use the set of transformations which form the group of symmetry operations of the square:
These are not contractive affine maps but by adding the condition that the range block has to be shrunk down onto the domain block they can be made to be contractive. Now we have an automatic compression algorithm:
You can see that the resulting fractal compressed image is just a list of range block positions and transformations. To reconstruct the image you simply use this information to iterate the entire set of transformations on a starting image. The collage theorem guarantees that the attractor of the set of transformations is close to the original image. How good the compression is depends on how well the transformations manage to map the sections of the image in the range blocks to each domain block. As long as the original image is rich in affine redundancy the chances are that it will work well. If not you either have to increase the possible range of transformations or divide up the image into smaller blocks. That's about it - the method needs to be extended a little to cover grey level and colour images (see grey level compression) but the same basic method still works. The final touch is to use one of the standard data compression methods on the coefficients of the IFS - but this really is standard stuff. Fractal or JPEG compressionIf you actually try fractal compression out on real images then what you find is that compression ratios of 10:1 or better do not produce significant distortions. Also while the compression time is rather on the long side the decompression time is quite reasonable - after all it only involves iterating with linear transformations. Fractal compression's main competitor is the familiar JPEG standard. This is a compression procedure that makes use of a modified form of Fourier analysis. It also divides up the image into small blocks 8x8 pixels in this case. However rather than try to represent each block as an affine transformation of another (larger) block it uses a set of 2D sine waves. JPEG does produce good compression results but it is claimed that it is inferior to fractal compression methods. One of the reasons is that fractal methods are not scale dependent. You can decompress a fractal image to any resolution you like by choosing the size of the image that you iterate. Of course beyond a certain resolution the extra detail you will see will be artificial but the argument is that because of its fractal nature it will not be too "obvious" and the image will still look natural. A second advantage is that fractal compression doesn't share a defect that is inherent in the JPEG and all Fourier methods. The problem is that where there is a discontinuity in the image, i.e. a step from black to white, the sine functions which are used to approximate it simply cannot do a good job. Why? Well sine functions are all smooth and curvy and a discontinuity isn't and so trying to fit continuous functions to a discontinuity is like backing a looser! As long as you don't push JPEG to too high a compression ratio you will not notice the problem but if you do then what you will see is a blurring of the edge and a pattern that looks like an echo of the change. This is the classical Gibb's overshoot or "ringing" effect and there isn't much you can do about it. Of course fractal compression has no such problem representing a discontinuity. Even so, today Jpeg compression is almost universally used and many of the early claims for the powers of fractal compression made in the 1990s never really came to be. fractal compression takes longer to implement and in most cases the gain in compression ratio over Jpeg isn't significant. Also the claimed "better quality at higher resolution" also isn't really an issue. Today fractal compression is still being worked on but at the moment its a technology in search of a problem. The book Fractal Image Compression: Theory and Application (see side panel ) includes code for encoding and decoding images using fractals.
<ASIN:0849373646> <ASIN:0387942114> |
||||||||||||||||||||||||
| Last Updated ( Monday, 27 May 2024 ) |