| Introduction to Boolean Logic |
| Written by Mike James | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Tuesday, 11 March 2025 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Page 4 of 7
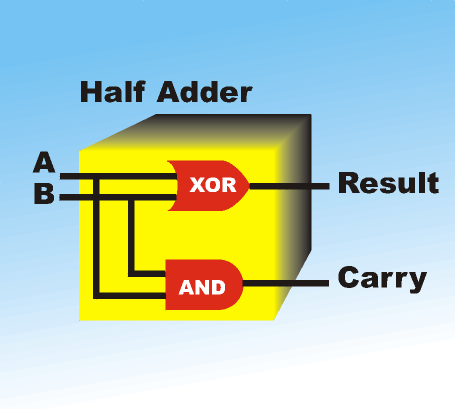
Binary arithmeticThe second connection that Boolean logic has with computers is actually just a special case of the first, but it is very important and it often confuses people. Boolean logic can be used to implement binary arithmetic. Notice that there is no suggestion that binary arithmetic and Boolean logic are the same thing - they aren’t. Binary arithmetic is just an example of a place value system for representing values. That is, we humans work in base 10 and computers find it easier to work in base two, because they don’t have ten fingers. However, when you do binary arithmetic you follow standard rules that determine how you should combine bits together to produce result bits. These rules can be expressed as combinatorial logic, in other words a truth table. You can easily construct a table showing how to add two bits together to give a result and a carry to the next place:
If you don't know how to add two bits together then simply accept that the table as your instructions for how to do it. You can see that this is just another truth table and the combinatorial logic needed for it can be produced in the usual way. Actually this is only a half adder - yes this is the real technical term - in that it doesn’t add a carry bit that might have been generated by a previous pair of bits.
The table for a “full adder”, this too is the correct technical term is:
The truth table can be converted into hardware: So combinatorial circuits are the main connection between Boolean logic and computer hardware but there is more to computer hardware than combinatorial logic. Occasionally you will hear computers referred to just one huge piece of Boolean logic but this is an overstatement. Large chunks are just And, Or and Not gates but there are also huge chunks that are not describable in terms of pure Boolean logic.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Last Updated ( Tuesday, 11 March 2025 ) |