| Inside Bitcoin - The Block Chain |
| Written by Mike James | ||||
| Thursday, 30 December 2021 | ||||
Page 2 of 3
Proof of work algorithmFor a programmer, the real puzzle about the whole Bitcoin scheme is the use of "proof of work". It simply doesn't seem to make technical sense. So much so that many have speculated that the need to do so much work is to give the Bitcoins created a real-world value. It is as if the CPU time and electricity put into validating a block is converted into the value of the Bitcoins that are created as a reward for the work. This doesn't seem to be the case but who really knows when it comes to assigning value to currencies - perhaps the difficulty of creating new Bitcoins is a psychological factor in their perceived value. In most cases proof of work algorithms are intended to slow down the rate at which an agent can access a service. For example, if you have a web service and you want to stop it from being overwhelmed by automatic clients you can set up an API which demands that each client solves a difficult but regular problem - like multiplying together two big numbers - before being allow to use the service. The client has to present the result of the multiplication as "proof of work done" and then it can use the service. This is not what proof of work is being used for in Bitcoin. The problem being tackled here is asynchronous update in a peer-to-peer system. For example, suppose you have a large group of people in a room and you need them to agree on a single time to meet the next day. The simple algorithm is to get them each to shout out the time that they have picked and the first to shout determines the time. Unfortunately in a distributed network there can be many "firsts". In the crowed of people who you hear as first depends on where they are positioned relative you you. This isn't about how loud they are but how long the signal takes to reach your ears. As a result the crowd doesn't reach a single decision on the time and they all arrive in bunches at the different times they heard first. It is also possible for a group of people to get together closer to you to shout a single answer that they have agreed on as a subgroup. What is the solution? One solution is to give each of the people in the room a random number generator which determines how many minutes to wait before shouting out their time. As long as the time interval between each number is longer than the time needed to propagate the signal across the entire network then most of the time only one person will shout out the time first and the entire crowd will agree on a time to meet. This is a true distributed way of arriving at a time - there is no central decision maker. However, there is a flaw in the protocol. If one of the people in the room is dishonest and wants to set the time of the meeting then they can cheat and shout out the time earlier than their random number generator tells them to. A better, but not perfect solution, is to give each person a difficult task to do. For example they might have to find a string that a hash function converts to the time they want to meet at. That is, given a hash function H find string such that H(string) equals the time you want to meet. This problem is difficult and it will take a different amount of time for each person to solve the problem (even if they all start at the same moment and use the best possible method). The result is that the time to complete the problem is more or less random and on average only one person will shout the answer first. Not only that but, by providing the string that solves the problem, they prove that they have done the work and not cheated. It is also difficult to see how the process could be subverted by a group of people co-operating because as long as the group is small in number there is a good chance that a group outsider will be picked. Proof of work in BitcoinThis is an interesting use of proof of work but what does it have to do with Bitcoin? The answer is that the act of validating a Bitcoin transaction is like having to pick a meeting time. You only want one valid block of transactions to make it into the database at a time. You also don't want the database to be modifiable after the transaction block has been validated and added. Imaging that a user makes two transactions with their Bitcoin with nearly identical timestamps - i.e. they are attempting to spend the same Bitcoin twice. If the transactions were processed on a first come first validated basis different parts of the network could see different transactions first with the result that both transactions could be validated. To avoid the double validation problem what happens is that Bitcoin nodes collect the transactions into a block and add a reference to the current final block in the database. They then verify that each transaction is permissible against the current database, i.e. that each transaction in the block is a possible transfer of a Bitcoin. The node then has to perform a complex calculation that will take an effectively random amount of time. The computation takes the form of adding an item of data to the block that makes its computed hash start with a specified number of zeros. A hash function is a complex function that takes a block of data and returns a long number. Usually this number is used to identify the data in some way or other. In this case the hash is just a target value. The node changes the value of one item of data in the block - the nonce - to create a hash that has It turns out that the amount of work required to do this is exponential in the number of zero bits. The only way to do the job is essentially trial and error and you also can't even guess how long it will take. The difficulty of the computation is adjusted as the amount of computing power available grows. On average it takes 10 minutes to solve the proof or work problem and the difficulty is adjusted to keep this time no matter how hardware or software advances.
Once the value has been computed it is added to the block and from this point on any changes to the block would require the work to be redone to make the hash have the correct number of zero bits.That is, the work both randomizes the moment that the block is submitted to the rest of the network as being valid and it signs the block so that it cannot be easily changed. The complete update showing two different nodes can be seen below:
Notice that at any one time there are a lot of nodes that are working on adding different blocks to the block chain. When one of them solves the proof of work problem they all drop the work they are doing on their blocks and accept the completed one. What happens next is the all of the nodes move on to add the next block. Transactions that haven't yet been added to the block chain are selected to make a new block and the whole process starts over. <ASIN:1491924543> <ASIN:1491920491> <ASIN:1785281976> <ASIN:1785287303> |
||||
| Last Updated ( Thursday, 30 December 2021 ) |
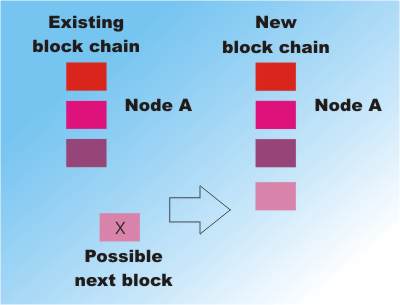 Adding a block after it has been validated and linked into the existing last block
Adding a block after it has been validated and linked into the existing last block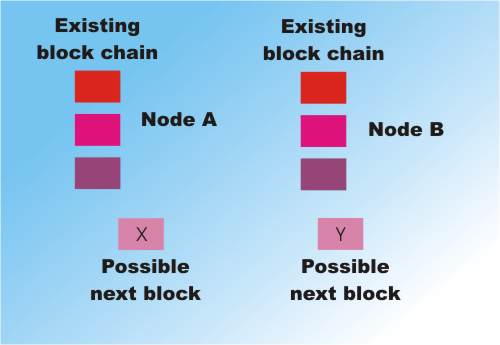 Two nodes work to solve two different blocks
Two nodes work to solve two different blocks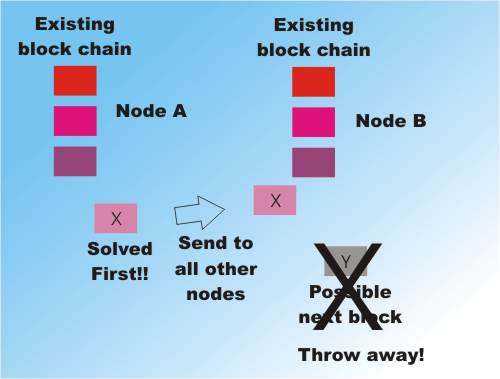 Node A completes first and sends its block out to all other nodes.
Node A completes first and sends its block out to all other nodes.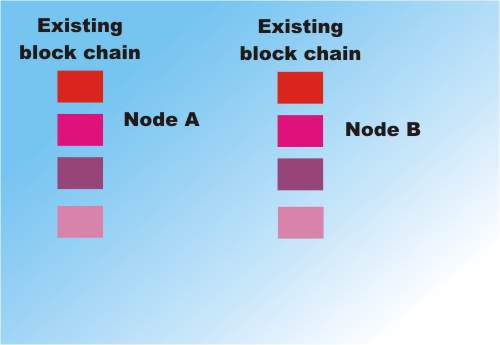 Which drop their candidate nodes and add the validated block to their copy of the database.
Which drop their candidate nodes and add the validated block to their copy of the database.