| Finite State Machines |
| Written by Mike James | |||||||
| Thursday, 18 January 2018 | |||||||
Page 3 of 3
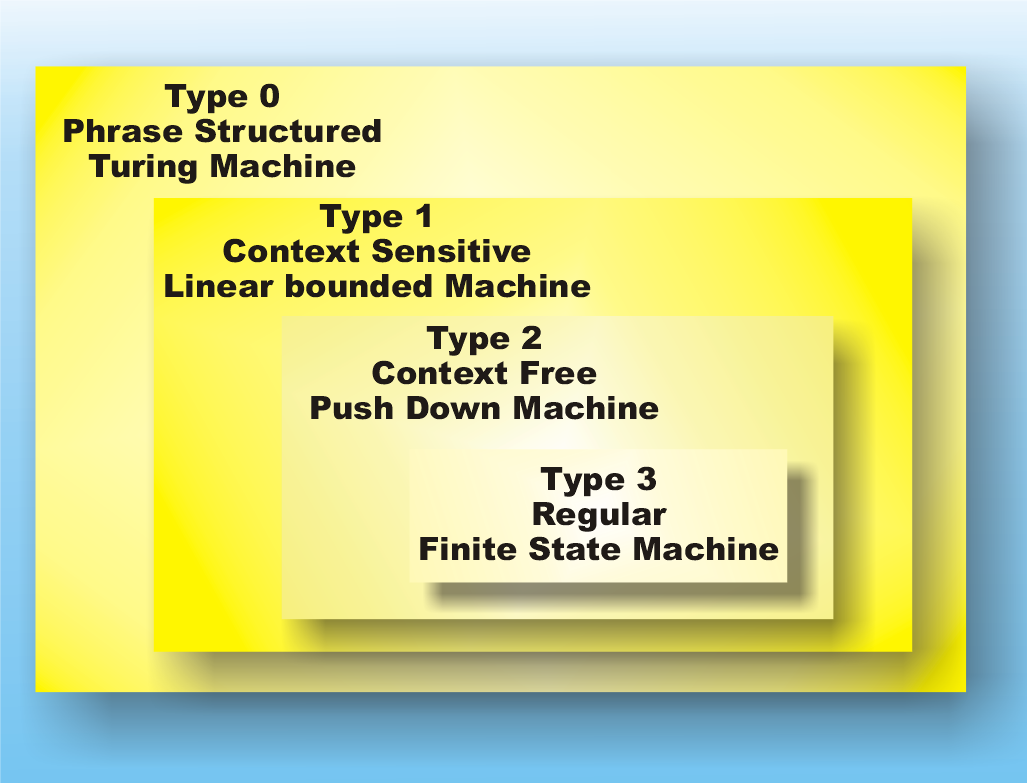
Turing machinesYou can probably guess that if the language corresponding to a push down machine is called context free the next step up is going to be ‘context sensitive’. This is true but the machine that accepts a context sensitive sequence is a little more difficult to describe. Instead of a stack, the machine has a ‘tape’ which stores the input symbols. It can read or write the tape and then move it to the left or the right. This is a Turing machine, which a lot of people have heard about even if they don’t know what it is. A Turing machine is more powerful than a push down machine because it can read and write symbols in any order, i.e. it isn’t restricted to LIFO order. However it is also more powerful for another, more subtle, reason. A push down machine can only ever use an amount of storage that is proportional to the length of its input sequence but a machine with a tape that can move in any direction can, in principle, use any amount of storage. For example, the machine could simply write a 1 on the tape and move one place left, irrespective of what it finds on the tape. Such a machine would create an unbounded sequence of ones on the tape and so use an unbounded amount of storage. It turns out that a Turing machine is actually too powerful for the next step up the ladder. What we need is a Turing machine that is restricted to using just the portion of tape that its input sequence if written on – a ‘linear bounded machine’. You can think of a linear bounded machine as a Turing machine with a short tape or a Turing machine as a linear bounded machine that has as long a tape as it needs. The whole point of this is that a linear bounded machine accepts context sensitive languages defined by context sensitive grammars that have rules of the form: anything1 -> anything2 but with the restriction that the sequence on the output side of the rule is as least as long as the input side. Consider A<S1>->A<S1>A as an example of a context sensitive rule. Notice that you can think of it as the rule <S1> -> <S1>A but only applied when an A comes before <S1> and hence the name “context sensitive”. A full Turing machine can recognise any sequence produced by any grammar – generally called a ‘phrase structured’ grammar. In fact a Turing machine can be shown to be capable of computing anything that can reasonably be called computable and hence it is the top of the hierarchy. Notice that a phrase structured grammar is just a context sensitive grammar that can also make sequences shrink as well as grow.
The languages, the grammar and the machines
That’s our final classification of languages and the power of computing machines. Be warned there are lots of other equivalent or nearly equivalent ways of doing the job. The reason is, of course that there are many different formulations of computing devices that have the same sort of power. Each one of these seems to produce a new theory expressed in its own unique language. There are also finer divisions of the hierarchy of computation not based on grammars and languages. However this is where it all started.
Further readingIt is difficult to pick further reading for finite state machines because there are so many books and most of them are at an advanced level. A really good easy to read classic is: Computation: Finite and Infinite Machines by Marvin Minsky but it is currently out of print. For an overview A Concise Introduction to Languages and Machines by Alan P. Parkes is fairly easy to read. You can see details of these books in the sidebar above. Related Articles.NET Regular Expressions in depth
Comments
or email your comment to: comments@i-programmer.info To be informed about new articles on I Programmer, sign up for our weekly newsletter, subscribe to the RSS feed and follow us on Twitter, Facebook or Linkedin.
<ASIN:1848001207> <ASIN:0131654497> |
|||||||
| Last Updated ( Tuesday, 24 August 2021 ) |