| The Trick Of The Mind - Turing Complete |
| Written by Mike James | |||
| Monday, 05 December 2016 | |||
Page 1 of 2 This second chapter of our new book-in-progress on the nature of programming is aimed at programmers and non-programmers alike. If you can't program, find out why you should learn. If you can program, find out why what you do is special and how it is a generally applicable thinking style. The Trick Of The Mind - Programming & ComputationalThoughtBuy Now From Amazon
Chapter List
What do you need to write a program? The answer has to be a programming language. What sort of language would that be? This time there isn't a short simple answer, or is there? In Chapter 1 we made the acquaintance of two programming languages - the language of geometry and the language of arithmetic expressions. Both of these were referred to as "little" languages because they are limited in ways we now need to make clear. A program is a list of instructions and the type of instructions in the list depends on the object that the program is working with. In the case of the geometric language the instructions were all about moving specified distances in specified directions. In the case of the little language of arithmetic the instructions were all about taking numbers and doing simple arithmetic on them. If the instructions that go into the lists are always different how can there be anything constant about programming languages? The answer is that any reasonably capable programming language always has the ability to make decisions and repeat things. For example, in a recipe you might find the instruction: "If the sauce is sweet add lemon" This is a conditional. You don't "add lemon" every time. Instead you compute a condition "is the sauce sweet" and if this true you "add lemon". The important point here is that the idea of a conditional is something you find in every programming language - even if it is well hidden. It is a universal of programming. Equally within a recipe you might find an instruction like: "Repeat the beating of the cream until it is thick" or: "Place 5 cherries on the top of the cake" In each case you are repeating an instruction. This repetition of an instruction occurs in every programming language and it too is a universal of programming. Sometimes it is hidden and difficult to see. For example, is "place 5 cherries" a repeat or just one action? For a human things are vague and you can think about instructions in different ways, but you can see that it is "place one cherry" repeated. You could say, even at this early stage, that it is the use of conditionals and repeats that makes a programming language so much more than a little language, but the ideas are so much bigger than just this. What we have observed so far is that there are common ideas in all lists of instructions. Even if the instructions change, the way that we can organize them to get things done stays roughly the same.
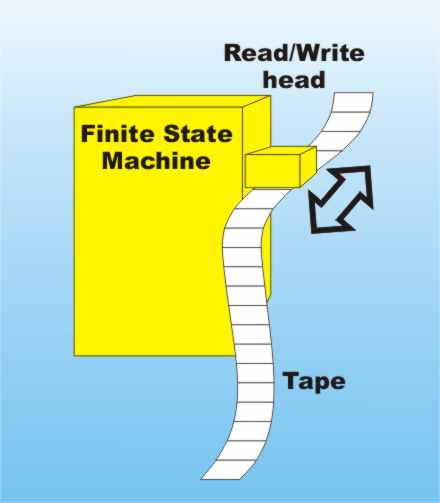
What is amazing is that these three options are all there is - there is nothing more sophisticated that can be thrown into this mix. All lists of instructions boil down to these three ways of obeying instructions. Programmers call the first the default flow of control, the second is a conditional and the third is a loop. At this point I need to introduce one other possibility - recursion. This is not the place to discuss it because it isn't easy to see what it is about and what makes it different from the other three. I only mention it here to allow for the possibility that you might have heard about it or know about and want to know where it fits in. The simple answer is that you don't actually need it because it can be reduced to some combination of the first three. This may be true, but recursion is still fascinating and of great practical value and there is a whole chapter devoted to it later. Turing CompleteDefault, loops and conditionals - is this all there is? The answer seems to be yes. You might think that there would be a hierarchy of programming languages. Simple ones for simple things and increasingly more advanced languages that can do things that were impossible in the earlier languages. This isn't the way the world is organized and rather than a hierarchy we are faced with a simple go/no go categorization. A programming language is either Turing Complete or it isn't. To understand what this means we have to take a small detour and find out what a Turing machine is. Alan Turing invented the most basic computing machine you can imagine. Essentially it was a simplified version of how a human might obey a list of instructions. The idea is that there is a paper tape. The human can read and write what is on the paper tape at just one place at a time and can move one place left or right on the tape. It sometimes helps to think of the tape marked up into squares and the human can only read or write into one square at any time. There is also a book of instructions that the human can read and each instruction tells the human to write something on the tape, move left or right or move to a new instruction in the book. There is a subtle detail that seems insignificant but it is very important and determines how powerful the Turing machine is. The paper tape is finite but if more tape is needed it can always be found. Mathematicians call this "finite but unbounded" and in this case it means that the Turing machine is not "resource" limited in what it can compute but it isn't physically unrealizable as it would be if we said the tape was infinite - how do you make an infinite tape? Of course you don't need a human to do this particular job and it is very easy to invent a mechanism that works without the intervention of a human - but Turing was trying to capture the most basic operation of a human obeying a program. A device that works as described is usually called a Turing machine after its inventor and you have to admit it is a very basic mechanism. To give you an example of a simple Turing machine consider the rules:
The entire tape is assumed to be blank when it is started and so the Turing machine writes 010101010101 ... and so on forever. This is a very simple Turing machine, but things can become much more complicated. You can, for example create a Turing machine that writes the digits of Pi on the tape or works out your total tax bill, assuming the tape starts off with the initial data. A Turing Machine - the yellow block labled "Finite State Machine" is the book of instructions that tells the machine what to write and how to move the tape. Turing hypothesized that his machine could compute anything that was computable. Today this is called the Church Turing thesis in honour of Alonzo Church whose work that was similar to that of Turing. Notice that you cannot prove that a mechanism like the Turing machine can compute anything that is computable, but to date no one has found an example that it cannot compute but something else can. In one sense you can think of the Turing machine as a definition of what it means for something to be computable. It is the very essence of computation. Even though a Turing machine is simple, and isn't the only way to define computation, it is the usual way of defining what is computable and what is able to compute it. So far every alternative definition of computation has been shown to be equivalent to a Turing machine. It is very important to be clear about what we are defining. If a Turing machine can compute something then it is Turing computable. The Church Turing hypothesis has nothing to do with what is or is not computable. It is that anything that is computable in any way is also Turing computable. That is a Turing machine captures the very essense of computing. Also notice that the Turing machine provides a test of how powerful a computing device or language is. If the device cannot compute something that a Turing machine can then it isn't as powerful. For example. the little languages in Chapter 1 cannot compute things that a Turing machine can. If a computing device can compute anything a Turing machine can then it is called Turing complete so our little languages are not Turing complete. To prove that something isn't Turing complete all you need is an example of something a Turing machine can compute and a proof that the device or language cannot compute it. Such a proof is often difficult. An even more difficult task however is to prove that something is Turing complete. To do this you have show that it can compute everything a Turing machine can - and this is an infinite task. Fortunately there is a shortcut to infinity in the form of simulation. If you can use the computing device or language to implement any Turing machine then clearly it can compute anything that a Turing machine can. Thus a language or computing device is Turing complete if it can be used to implement any Turing machine. This is an easier definition of Turing complete, but notice that it isn't enough just to show that you can use the language to implement a single, or even a few, Turing machines. You have to show that it is possible to implement any Turing machine. In this sense it is still an infinite problem. |
|||
| Last Updated ( Tuesday, 06 December 2016 ) |