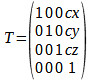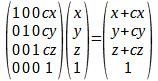| JavaScript Canvas - WebGL 3D |
| Written by Ian Elliot | ||||||
| Monday, 06 December 2021 | ||||||
Page 2 of 5
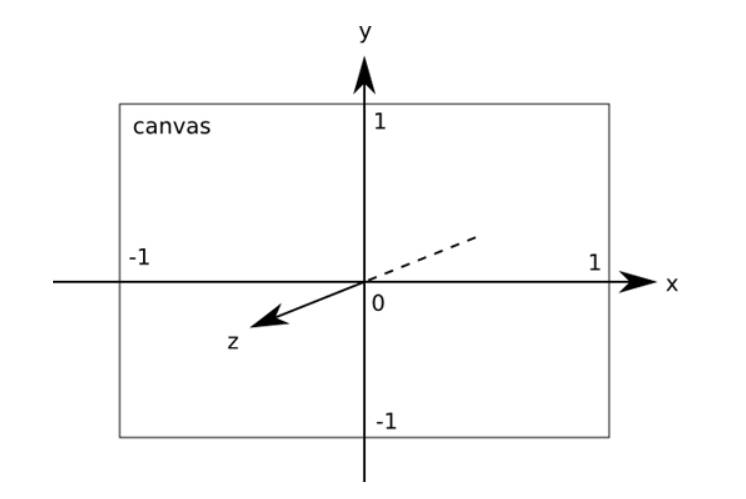
Vertex ShaderThe key idea here is that the WebGL drawing context is 2D. If you want to render 3D graphics then you have to supply the math that converts the 3D points to 2D canvas points. The only co-ordinate system that WebGL uses is shown in the diagram below:
The first shader that you have to set up, the vertex shader, controls how the co-ordinate system you are working with is mapped to the canvas. In general, it has to reduce the 3D co-ordinates that you are using in “model space” to the 2D co-ordinates. This is usually done in two steps. First a “projection” matrix is used to convert the 3D points to a 2D representation that “looks correct”. In most cases a perspective transformation is applied giving a 2D representation where objects that are further away in the z dimension are smaller. After this a 2D transformation is used to scale, rotate and skew the model co-ordinates into the canvas co-ordinates. You also need to know that WebGL works with homogeneous co-ordinates. That is, any point you want to plot on the canvas is specified as: (x,y,z,1) If you look back to Chapter 5 you will see that the 2D context also uses this form of position and for the same reason. Homogeneous co-ordinates make it possible to use a single matrix to specify scaling, skew and rotation and translation. For example, a transformation matrix like:
when multiplied by a homogeneous vector, gives:
You can see that the effect is to move the point by cx,cy,cz. Without homogeneous co‑ordinates you would have to deal with translation as a special case. There is a second reason for working with homogeneous co-ordinates. As a final step before the x.y values are plotted in 2D they are divided by the fourth dummy co‑ordinate. As in standard form a homogeneous co‑ordinate has a fourth co‑ordinate that is 1 this usually makes no difference, but a perspective transformation produces a final co‑ordinate that is different from 1 and in this case the division does make a difference. In general in a transformation that attempts to represent depth on a 2D canvas, the fourth co‑ordinate is proportional to z and so things that are further away, large z, are divided by a larger fourth co‑ordinate and so are drawn smaller, more about this a little later. The vertex shader we are going to use at first is one you will find in most introductions to WebGL and is a perspective transformation followed by a co-ordinate transformation: Canvas coordinates = Perspective Transformation *
Model Transformation * vertex coordinates
Shaders are specified using GLSL (OpenGL Shading Language) which is basically C with additional data types and standard functions. We don't have space to go into the details of GLSL, but you should be able to understand roughly what our basic shaders are doing. Notice that WebGL1 supports GLSL ES 1.0 whereas WebGL2 supports both GLSL ES 1.0 and GLSL ES 3.0. These are all older than the current version of GLSL used in modern OpenGL systems and there are differences. As already stated, for reasons of compatibility and because Safari doesn’t currently support WebGL2, the rest of this chapter uses GLSL ES 1.0. The differences are minor. Our “standard” vertex shader is: attribute vec3 vertexPosition;
uniform mat4 modelViewMatrix;
uniform mat4 perspectiveMatrix;
void main(void) {
gl_Position = perspectiveMatrix * modelViewMatrix *
vec4(vertexPosition, 1.0);
}
The first three lines define some data structures. The vertexPosition is a 3D vector, vec3, which specifies a location in model space. If you are using WebGL 2 then the shader is: #version 300 es
in vec3 vertexPosition;
uniform mat4 modelViewMatrix;
uniform mat4 perspectiveMatrix;
void main(void) {
gl_Position = perspectiveMatrix * modelViewMatrix *
vec4(vertexPosition, 1.0);
}
where attributes are now declared as in variables. Note that #version 300 es is required and has to be the very first line. An attribute is a value that is supplied to the shader from your program via a buffer. Buffers are arrays of data that you supply to WebGL and are used when you ask it to draw the buffer. Attributes determine how to read that data and your vertex shader is called repeatedly to process the items of data in the buffer. You can think of this as an implied loop reading the data in the buffer and processing it until the buffer is used up. There are a number of predefined attributes, but in this case we are going to supply these attributes after we create the buffer defined as the x,y,z co‑ordinates that specifies the points to be drawn. The two matrices are also going to be supplied to the shader later. The uniform qualifier means that these quantities don't vary with the vertices being read from an attribute buffer. That is, they are very much like simple parameters passed to the vertex shader in the sense a uniform has the same value each time the shader is called to process an item of data in the buffer associated with an attribute. If the attribute is like an implied for loop reading and processing the buffer, then a uniform is a variable that is constant for the entire loop. There is one modelViewMatrix and one perspectiveMatrix for each call of the shader while it is processing the items in the buffer associated with vertexPosition. The gl_Position variable is standard and supplied by the system that sets the position of the vertex using the fundamental co‑ordinate system. As well as uniforms and attributes, there are other types of data you can pass into your shaders and you can also use simple local variables within a shader as temporary storage. Notice the uniforms and attributes are read-only in the shader. To be clear, when you ask WebGL to draw the contents of a buffer, the vertex shader is called for each element in the buffer with the same values for the uniforms. |
||||||
| Last Updated ( Monday, 06 December 2021 ) |