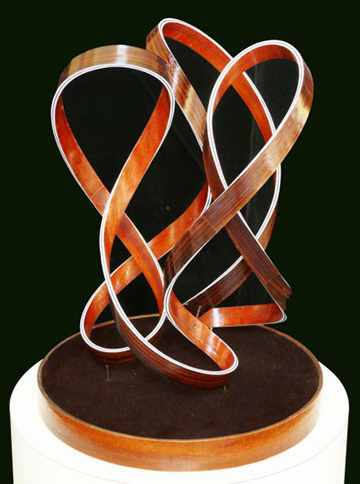| Mathematical Art 2019 |
| Written by David Conrad | |||
| Sunday, 02 June 2019 | |||
|
There is a deep affinity between math and art. There is beauty in mathematical symbols and the forms that they describe. Every year the American Mathematical Society (AMS) organizes an art exhibition and awards prizes. Looking for the results of the 2019 Mathematic Art Exhibition led me to the Mathematical Imagery section of the American Mathematical Society website which now almost 50 exhibits from recent shows, making it hard to choose the most impressive. The Klein bottle above from Elizabeth Paley was the winner of the Best textile, sculpture, or other medium for 2019 and is a recognizable example of a mathematical object. This piece is titled "Three Dancers" and its originator, Fielding Brown, explains: This sculpture demonstrates my technique of building 3D-Lissajous figures. I first saw these figures on the screen of an early oscilloscope, flat curves describing, for example, a spinning coin or a gyrating hula hoop. I then imagined how I might describe these Lissajous in 3D, and then how to actually build them as sculpture.
Wood features again, together with cotton in this work from David H Press who writes: I am dedicated to fully exploring the possibilities of three dimensional shapes formed by straight lines. Symmetry makes it easier to suspend a form in midair as the forces pull it in all directions equally. Moving away from 3D to 2D, this work and comes from Hans Dehlinger who says: The focus of my work is on generative art based on algorithms. This image is based on the numbers 1 - 1 - 2 - 3 - 5, which are at the beginning of the well known Fibonacci Sequence. Mathematically it is rather simple - however, quite amazing opportunities from an artist´s point of view are resulting. The underlying line-drawing is generated with a program (Python), and its parameter settings determine angle, number of lines in sections, repetitions, rotations, and so on. The mathematical starting point and the strict generative-algorithmic production process are on the one side; the addition of intuitive artistic judgement is on the other side.
For a "blast from the past" here's another algo-based print form David Thompson who explains: This artwork was created with MatLab and Stipple Generator software with technical assistance from Dr. Timothy Chartier, Professor of Mathematics and Computer Science at Davidson College. The algorithm that Chartier's MatLab program used was based on the Traveling Salesperson Problem and is compatible with any digital image. I used the program to create this TSP art in memory of my former professor Dr. Reza Sarhangi (1952-2016), who was a Professor of Mathematics at Towson University, and he taught me while I pursued my undergraduate and graduate studies in secondary mathematics education. Pollen Form from Robert Fathauer is an example of the way in which mathematical structure is evident throughout the natural world. The artist, who works in ceramics writes: My work explores the mathematics of symmetry, fractals, tessellations and more, blending it with plant and animal forms as well as inorganic forms found in nature. This synthesis allows me to create innovative prints and sculptures that derive their beauty from a combination of complexity and underlying order. This piece was inspired by electron micrographs of pollen grains such as dandelion, chicory, and stitchwort. It has approximate icosahedral symmetry.
There's plenty more to explore on the site so if you need inspirations, or just like browsing art, you know where to go. More InformationRelated ArticlesAI-Generated Painting Sells For $432,500 - A Deep Misunderstanding To be informed about new articles on I Programmer, sign up for our weekly newsletter, subscribe to the RSS feed and follow us on Twitter, Facebook or Linkedin.
Comments
or email your comment to: comments@i-programmer.info |
|||
| Last Updated ( Sunday, 02 June 2019 ) |