| Neural Networks Learn to Produce Random Numbers |
| Written by Janet Swift |
| Wednesday, 10 October 2018 |
|
It almost sounds silly - train a neural network to generate random numbers - but it has more practical uses than you might imagine. Intelligent systems are bad at generating random numbers. They may well be pattern detectors, but they also often see patterns where none exist. Is 123456 more or less random than 324516? After all, they both have the same probability of being generated by a truly random number generator! Humans when asked to generate a random number generally try for something that seems disordered and tend to leave out ordered sequences that would occur in a true random number generator. In computing we tend not to use physical sources of true random numbers. Instead we use pseudo random number generators or PRNGs. These are mathematical functions that create sequences of numbers that not only look random but pass statistical tests to make sure every sequence of numbers occurs equally often. You might be able to guess that constructing a good PRNG isn't easy and one that passes enough tests to be considered secure, i.e. a cryptographic PRNG, is even harder. Good PRNGs are important for all sorts of statistical techniques, but in particular they are important in security applications. Given a neural network can be regarded as a big function approximator why not just train a neural network to generate the output of a PRNG? This sounds like a good idea, but then you would only get a neural network that was as good as the PRNG used to train it. The idea, using real random numbers, was tried and found to be not particularly effective.
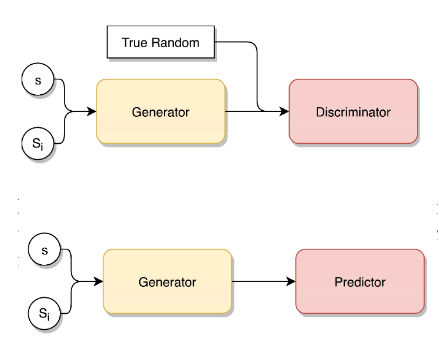
A much better idea is to use a Generative Adversarial Network, or GAN, or a modification of a GAN into a generator/predictor pair of networks. What happens is that the generator portion of the network - a standard feedforward network - generates a sequence of n bits and the predictor network is given n-1 bits and tries to predict the last bit. The generator tries to maximize the probability that the predictor will get it wrong and the predictor tries to get it right. So the idea is that the generator has to beat the predictor as it gets better and better at predicting the pseudo random sequence. You really can think of this as being like a competition between two humans - one tries to create random digits and the other tries to guess them. In fact, it is a lot like the actual competitions involving the game of rock, paper, scissors where basically one player is trying to generate an unguessable sequence and the other is trying to guess it. Of course, we are not talking about human brains locked in conflict, just a pair or relatively small neural networks. Did it work? "We demonstrate that a GAN can effectively train even a small feed-forward fully connected neural network to produce pseudo-random number sequences with good statistical properties. At best, subjected to the NIST test suite, the trained generator passed around 99% of test instances and 98% of overall tests, outperforming a number of standard non-cryptographic PRNGs." So not up to cryptographic PRNGs yet, but it is surprising that randomness can be learned. Given that the networks are feedforward only, and nearly all PRNG function involve some feedback, it might be that some sort of recurrent network is required. With some more work it is possible that handcrafted PRNGs might be a thing of the past and AI will have made another, albeit niche, area of human endeavour redundant.
More InformationMarcello De Bernardi, MHR Khouzani and Pasquale Malacaria
Queen Mary University of London Related ArticlesERNIE - A Random Number Generator How not to shuffle - the Knuth Fisher-Yates algorithm Canada's RAND Immigration Lottery Not Random! Random Means Random - The Green Card Fiasco Randomness Restored In Chrome 49 To be informed about new articles on I Programmer, sign up for our weekly newsletter, subscribe to the RSS feed and follow us on Twitter, Facebook or Linkedin.
Comments
or email your comment to: comments@i-programmer.info |
| Last Updated ( Wednesday, 10 October 2018 ) |