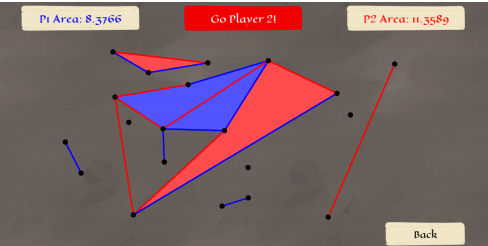
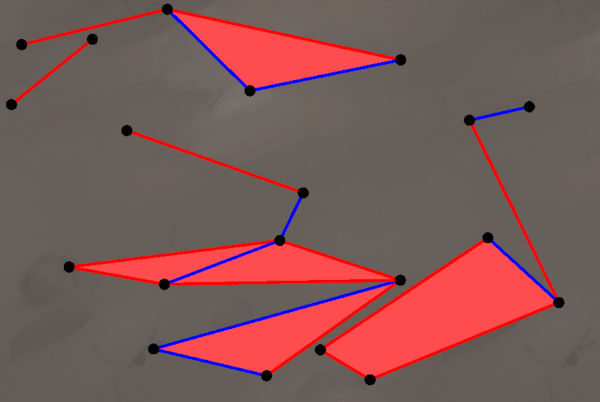
OK, new proofs that things are NP hard are so common that we have given up reporting on them, but this one - a new game from the Department of Mathematics and Computer Science at Eindhoven University of Technology - is fun. It's a generalization of the well-known Dots and Boxes.

It is true that given a task with even a moderately big search space it turns out to be NP hard - no great surprise there. This particular piece of research, however, introduces a variation on a  Dots and Boxes to become Dots and Polygons. Not as catchy a name, but more interesting.

If you have played Dots and Boxes you will know it as an irritating game that you can lose simply by not concentrating enough because it seems such a simple task. Given a regular grid of dots all you have to do is connect adjacent dots with a straight line and attempt to complete a square. As players take it in turns it has the feel of Nim, where each player tries hard not to leave a 3-sided box for the next player to complete.

The generalization Dots and Polygons is played on a set of points in the plane. Each player takes a turn at drawing a connection line that doesn't intersect any other point or any existing edges. The objective is to form a closed polygon and the overall winner is the one with the maximum area covered by polygons. Two variations on the game are Dots and Polygons and Holes, where polygons are allowed to contain other polygons, and Convex Dots and Polygons where they have to be convex. If you try the game you will quickly discover that the "no intersect" rule is a big part of the strategy in not leaving two sides that your opponent can connect. You can try all three versions out at:

https://www.win.tue.nl/~kbuchin/proj/ruler/dotsandpolygons/

but notice that it only allows human against human. An interesting project would be to train a neural network to play the game as playing it needs spatial reasoning as well as logic - a sort of easier Go. The source code is also available.

The key result of the research  is that deciding if a win is possible in Dots and Polygons is NP hard - you can find the details in the paper, authored by Kevin Buchin, Irina Kostitsyna et al.

If you are keen on such things then you might like the final theorem:

Theorem 5. Let P be a set of n points in the plane in convex position. For n = 3, 5, 7 player R can score at least half of the area, for n = 4, 6 player B can score at least half of the area.

The problem for n>7 is open.

• Mike James is the author of The Programmer’s Guide To Theory which sets out to present the fundamental ideas of computer science in an informal and yet informative way and devotes a chapter to a discussion of what makes a problem NP-hard.

More Information

Dots & Polygons

Kevin Buchin, Mart Hagedoorn, Irina Kostitsyna, Max van Mulken, Jolan Rensen and Leo van Schooten

https://www.win.tue.nl/~kbuchin/proj/ruler/dotsandpolygons/

Related Articles

1×n Jigsaw Puzzles are Hard

Pancake flipping is hard - NP hard

Rubik's Cube Is Hard - NP Hard

Physics Is NP Hard

Tensor Operations Are NP Hard

Candy Crush Is Harder Than It Sounds - NP Hard

Travelling Salesman - A Movie About P=NP

To be informed about new articles on I Programmer, sign up for our weekly newsletter, subscribe to the RSS feed and follow us on Twitter, Facebook or Linkedin.

Comments

Make a Comment or View Existing Comments Using Disqus

or email your comment to: comments@i-programmer.info

<ASIN:1871962439>