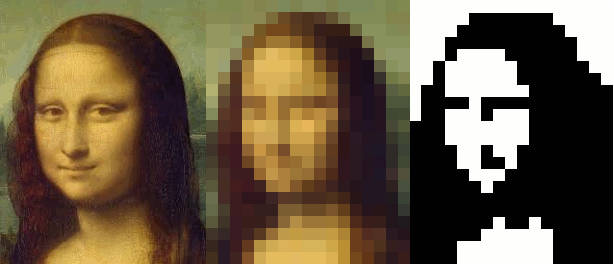| Finding The Mona Lisa In Life |
| Written by Mike James |
| Saturday, 21 March 2020 |
|
This is a fun project that may well suggest interesting follow ups. And you don't have to be an expert on the Game of Life to join in. Cellular automata are fascinating because they give rise to such complex behavior from such simple rules. John Conway's Game of Life GoL is perhaps the best known and it is astonishingly complicated given how simple its rules are. What is even more astonishing is the time and effort people put into finding configurations of cells that achieve particular behaviors. If you take an image and digitize it to binary then you can regard this as a starting point for a GoL configuration. Take the Mona Lisa for example. Digitizing it gives:
You can then run the simulation and see what happens. As blocks of live cells next to each other die at the next step you almost immediately get an outline and then configurations which slowly decay and look less and less like the original. What about the problem of finding a configuration that evolves into a well known image? This is the problem that Kevin Galligan tackles on his personal blog. If you think this is easy then you probably haven't noticed that GoL is not a reversible cellular automaton. You can't easily go backward in time from a configuration you want to an earlier configuration that evolves into it. However, what you can do is write down a Boolean equation that gives the state of the grid in terms of what it would have to be to generate the current state. For example, if the cell is alive then if it was alive in the earlier state it must have 2 or 3 alive neighbours, but if it was dead then 3 of its neighbours must have been alive. You can write this down as a logical equation involving the states of the cells. The big problem is that this equation is big and difficult so solve. You have to find values of all of the variables that make the equation true. If you have a passing acquaintance with computer science theory you will recognize this as a SAT problem and there are automatic SAT solvers which we can use. However, SAT is an NP Complete problem and this makes it one of those problems that very quickly becomes too big to solve. Nevertheless you can work with 400 cells in something like 250 seconds. So you can take a state and write down the logical equation for the state that will evolve into it in one time step. You can then take that state and write down its logical equation and solve for the state that came before it, and so on. Problem solved! Not quite. There can be multiple solutions at each step and there can be no solution at all. Some configurations are called "Gardens of Eden" because you can prove (not easily) that there is no configuration that evolves into them. It seems that these are more common than you might imagine and hence difficult to avoid. All but one of the images that were tried resulted in a Garden of Eden at the very first backward step. To return to the digitized Mona Lisa, what do you think the configuration that evolves into it after just one step looks like?
Not much trace of the the original! Have a look at Kevin's blog for more examples. Why so many Gardens of Eden? Even if you don't find this fun at least you now know what you can use a SAT solver for.
More Informationhttps://kevingal.com/blog/mona-lisa-gol.html Related ArticlesTetris On Game Of Life - A Great Achievement SmoothLife - A Continuous Conway's Life Cellular Automata - The How and Why Waterbear Spaceship - Conway's Life A New Computational Universe - Fredkin's SALT CA To be informed about new articles on I Programmer, sign up for our weekly newsletter, subscribe to the RSS feed and follow us on Twitter, Facebook or Linkedin.
Comments
or email your comment to: comments@i-programmer.info
|
| Last Updated ( Saturday, 21 March 2020 ) |