| Training A Cellular Automaton |
| Written by Mike James | |||
| Sunday, 16 February 2020 | |||
|
Put cellular automata together with neural networks and you might be able to grow a salamander - or anything else you like. This work, from Google AI, casts much light on the difficult topic of morphogenesis, how cells organize themselves into shapes. The mystery of how biological cells form the complex shapes that we take for granted, us for example, is difficult to even get a start on. We may understand DNA and the genetic code but we have a very poor grasp of how this determines the structure of multi-cellular animals. We have some idea that it is all about chemical gradients which cause cells to behave in different ways, but so far we don't understand even the general principles involved. This new research is led by Alexander Mordvintsev, the creator of DeepDream, Google's computer vision program and sprang from the idea of applying neural networks to understanding regeneration and to designing self-organising systems proposed by Michael Levin, Director of the Allen Discovery Center at Tufts University. It combines two of my favourite topics - cellular automata (CA) and neural networks and it aims to explore how simple rules give rise to complex organization. The idea is simple but ingenious and it is worth knowing about just because it is fun.
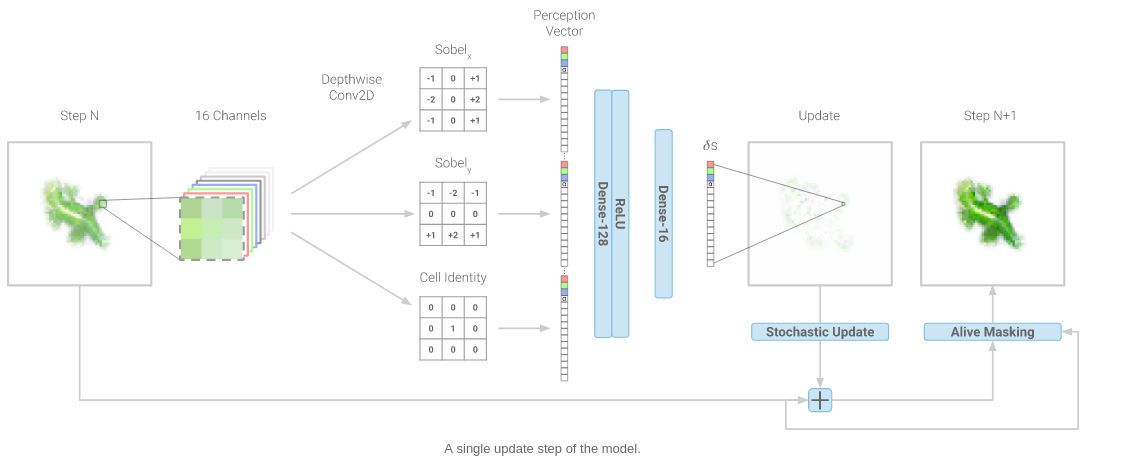
It seems reasonable to explore what can be achieved if each entity, a cell, follow a single rule. The question is what sort of rules can be used to create a given end result. For example, if you think of an array of black or white pixels displaying a square or a circle then you can convert this to an outline by telling each pixel to look at the color of their neighbors - "if you are black have a neighbor that is white then stay black otherwise change to white." This single rule obeyed by each pixel immediately picks out all the pixels in the border or the shape and so transforms it to its outline. Notice every pixel obeys the same rule, but they don't all do the same thing. Also notice that while we succeed in picking out what looks like a global property, i.e. the outline, each pixel acts locally. This sort of uniform rule is what characterizes cellular automata. Each cell in the grid is given the same rule which involves the cell's state and the state of the cells around them. Such a rule is local but, as proved by Conway's Game of Life, it can result in very complex organized behavior. The question is can we find simple rules obeyed by every cell that can produce a given complex shape? This is what the new research is all about. The key idea is that system has to be differentiable so that a gradient can be derived and used to modify the rule to move the system towards a better result. This is how back propagation works and how neural networks learns, but it is a more general idea that allows more complex systems to "learn" to do better. In this case we have a grid of cells and each one has a 16-element state vector which represents the cell's current physical state. The first four elements are an RGBA color specifier and it is the RGB values that we are going to use to train the system to find a rule that produces a given configuration. The alpha channel is used in a fairly standard way with 1 as a foreground pixel and 0 as a background pixel. In addition cells with an alpha less than 0.1 and with no neighbours with higher values are considered as dead and have their state vector set to zero at each time step. Cells that have an alpha<0.1 but do have live neighbours are considered as growing and do take part in the computation. This produces an outer "skin" or cells that are in the process of maturing. Now we have an array of cells each with a 16-dimensional state vector with the first four elements giving the visual appearance of the cell. The remaining 12 elements are intended to model things like concentrations of chemicals and it is these that are going to be modified by the update rule in ways that produce the target shape we are trying to produce. The next part of the procedure is to train a neural network to find a "rule" that combines a cell's state vector with those of its neighbours to produce a new state vector. Notice that the neural network represents a single rule applied to all of the cells in the same way - it is the sort of cellular automaton rule we are looking for. There are lots of practical details outlined in the paper, but the most important if you are interested in getting the general idea is that the information about the neighbors that is sent to the neural network is the difference in the state vectors plus the cell's state vector. The gradient is taken in the x and y directions and thus we are feeding the neural network a 48-dimensional vector summarizing the state of each cell and the gradient around it in turn. The neural network is only provided with information on the gradient of the state vector. This is intended to model the fact that biological cells often respond to chemical gradients rather than absolute values. The neural network has 8000 parameters and so is capable of learning a fairly complex function of the neighbor gradients and state. It is interesting to ask how much of this complexity is actually used in producing biologically plausible configurations.
The system is given a target configuration and an initial "seed" configuration and then gradient descent is use to learn a rule that will evolve the seed into the target. Three main variations on the initial experiment, in which the network is trained to find a rule that evolves the seed to the target, are reported. The first finding is that the simple learning experiment works quite well, but when the system is iterated beyond the point of achieving the target configuration the shapes continue to grow or die out. In other words, the learned rule achieves the shape, but it isn't stable. This clearly wouldn't do in the real world unless there was a switch to turn the rule off when the final configuration was achieved. The second experiment addressed the need for a stable system by training beyond the point where the target configuration was achieved. There are lots of fine details about the implementation, but it does seem to achieve a rule that gives a stable pattern - a rule that has the target as an "attractor" for its dynamics. The third experiment also trained on an ability to regenerate. When the target pattern was achieved parts of it were damaged and the network trained to regenerate the target. This is interesting as a rule that has the target as an attractor would likely have regenerative properties. This work suggests so many additional questions that it is clearly just the start of something. What it demonstrates is that a 16-dimensional state vector is enough to allow a CA-type rule to evolve to complex shapes with a good degree of stability and regeneration. What these dimensions might represent in the real world is a question for the biologists. What I'd like to know is how many dimensions are necessary for it to work at all? Read the paper and look at the live code examples for more details.
More InformationGrowing Neural Cellular Automata Alexander Mordvintsev, Ettore Randazzo, Eyvind Niklasson and Michael Levin Related ArticlesCellular Automata - The How and Why A New Computational Universe - Fredkin's SALT CA A Computable Universe - Roger Penrose On Nature As Computation Turing's Biological Pattern Theory Proved To be informed about new articles on I Programmer, sign up for our weekly newsletter, subscribe to the RSS feed and follow us on Twitter, Facebook or Linkedin.
Comments
or email your comment to: comments@i-programmer.info |
|||
| Last Updated ( Sunday, 16 February 2020 ) |