| What Is Really Going On In Machine Learning? |
| Written by Mike James | |||
| Wednesday, 28 August 2024 | |||
|
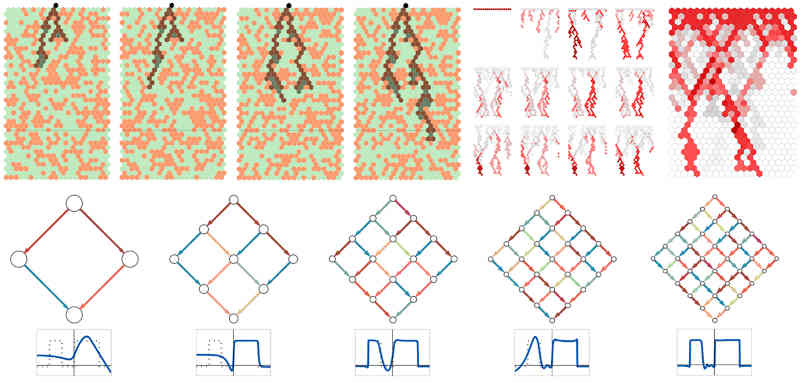
Stephen Wolfram has just produced a very long blog post with the title "What’s Really Going On in Machine Learning? Some Minimal Models". Is it possible he knows? In my opinion, no and, more strongly, it doesn't even get off the starting line. This said, the approach is interesting and it's a good read. The point is that we really already know why neural networks, which is what he means by "machine learning", work. They are the application of the simple principle of optimization coupled with Ashby's Law of Requisite Variety, which basically says that a system must be as variable or complex as its environment to succeed. It is an old law from the early days of cybernetics, what ever happened to that particular endeavor? Extending it a little it says that if a system has a particular number of degrees of freedom then any system that hopes to control, mimic or act in opposition to it has to have the same number of degrees of freedom or more. The principle of optimization is roughly that if you keep moving those degrees of freedom in the direction of "better" then you will eventually get to a state that is acceptable. Deep neural networks are systems that have a huge number of degrees of freedom - so many in fact that they are comparable with the degrees of freedom inherent in the real world or at least a constrained subset of such. The optimization comes in the form of back propagation, which is itself just an application of the slightly more general gradient descent. Basically this works by taking the derivative of the system, i.e. finding how to adjust the parameters to reduce the error and then moving things in that direction. Gradient descent is just the mathematical expression of "if you keep moving downhill you are very likely to reach the bottom". These are such powerful simple ideas that you can quickly come to the conclusion that if you can implement something as a complicated enough differentiable system then you can train it to do almost anything. For example, if you can change the discrete and non-differentiable approach to programming to something smooth and differentiable then you can use gradient descent to learn to program, see DeepCoder Learns To Write Programs. The latest blog by Wolfram goes into how to use cellular automata to learn functions. Before he gets onto that topic, he illustrates how a standard neural network learns by reducing the model to something that is simple enough to allow the tracing of its evolution. This is interesting, but not revealing of what we all really want to know - does the network capture some "essense" of what it learns or is it just remembering it without reduction to something simpler? The really interesting part of the blog, although it doesn't really answer the question posed at the start, is where the neural network is replaced by 1D cellular automata. In this case, learning is achieved using a modified genetic algorithm.This algorithm is a discrete version of the optimization principle that operates without a gradient. This is because the concept of a 'derivative' doesn't exist in discrete systems. Instead, the algorithm uses random exploration of the response surface. It is the equivalent of going down a hill by tentatively moving in each direction to find out which one is "down" and then moving in that direction. You find the gradient by exploration of the region close around you. The next idea is to use cellular automata that are restricted to Boolean rules and vary these rules to get different behaviors. You can induce learning by selecting a set of rules to apply in order - a sort of program. You can then train them using a form of genetic algorithm to reach a final outcome. Guess what? It works! Again, the optimization principle combined with Ashby's triumphs. Are we any closer to understanding why neural networks are so effective? Not really but it is fun.
You can also consider the "new" cellular automata networks as examples of Kolmogorov-Arnold networks, KANs. Standard neural networks have a fixed set of functions implemented by all the neurons and the learning is performed by adjusting the weights of each function. That such a network can learn to reproduce any function is a consequence of the universal approximation theory, which says that, for the right network function, even very simple functions can be adjusted to get close to any more general function. The Kolmogorov-Arnold representation theory says something similar, but in this case we use different functions at each neuron. If you think of a rule as the equivalent of a function, it is a Boolean function, then we have a KAN network. The blog then goes on to try to relate all this to the principle of universal computation, which roughly says that just about every system that isn't trivial is highly likely to be Turing complete - i.e. capable of computing anything. Well all this is true and if you put the principle of universal computation together with the principle of optimisation and Ashby's law, things start to make sense. We are still no closer to understanding neural networks - but the blog post is fun to read and thought-provoking, as long as you don't assume that everything you read is new and unconnected to other research. The real issue with neural networks is not how they learn - that's fairly easy to understand and there is even a reasonably good mathematical foundation for it. What is interesting is how a deep neural network represents the world it is being trained on. Are the clusters, groupings and so on in the real world mirrored by structures in the trained network? And do these structures allow generalization? Now answer these questions and we have made progress.
More InformationWhat’s Really Going On in Machine Learning? Some Minimal Models Related ArticlesNeurons Are Smarter Than We Thought Neurons Are Two-Layer Networks Geoffrey Hinton Awarded Royal Society's Premier Medal Evolution Is Better Than Backprop? Hinton, LeCun and Bengio Receive 2018 Turing Award DeepCoder Learns To Write Programs. Automatically Generating Regular Expressions with Genetic Programming To be informed about new articles on I Programmer, sign up for our weekly newsletter, subscribe to the RSS feed and follow us on Twitter, Facebook or Linkedin.
Comments
or email your comment to: comments@i-programmer.info |
|||
| Last Updated ( Wednesday, 28 August 2024 ) |