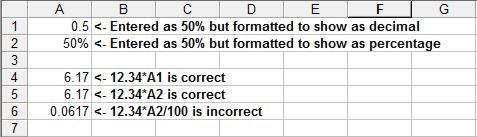
Spreadsheets and percentages

The fact that it is easier to work with fractions and easier to interpret percentages causes no problem to a spreadsheet user.

The reason is that nearly all spreadsheets allow you to enter a fraction and display it as a percentage. That is, if you format a cell or range to display as percentages, entering a fraction such as 0.5 will result in 50% being displayed.

This can be the cause of confusion if you are not aware of what is happening.

To make what you enter the same as what is displayed, most spreadsheets will also allow you to enter a percentage using a percent sign.

For example, if you enter 75% then 0.75 is stored in the cell but, as long as a percentage format applies, it will display as 75%. In this case it really is possible to forget what is stored in a cell. The danger is that you will make the mistake of including 100 in all formulas that make use of the apparent percentages. Notice that if you don’t set a percentage format then in nearly all cases a percentage will display as a decimal fraction.

Formatting avoids errors

In the figure above you can see a percentage entered with and without being formatted as a percentage. When trying to work out 50% of the value 12.34 you can see that the temptation is to enter =12.34*A2/100 because A2 looks like a percentage.

Of course it isn’t a percentage and so the correct calculation is just =12.34*A2.

That is:

• Always enter a percentage value with a trailing percentage sign
  
  
• Always format cells that contain percentages to show as percentages
  
  
• Always calculate using percentages as if they were decimal fractions

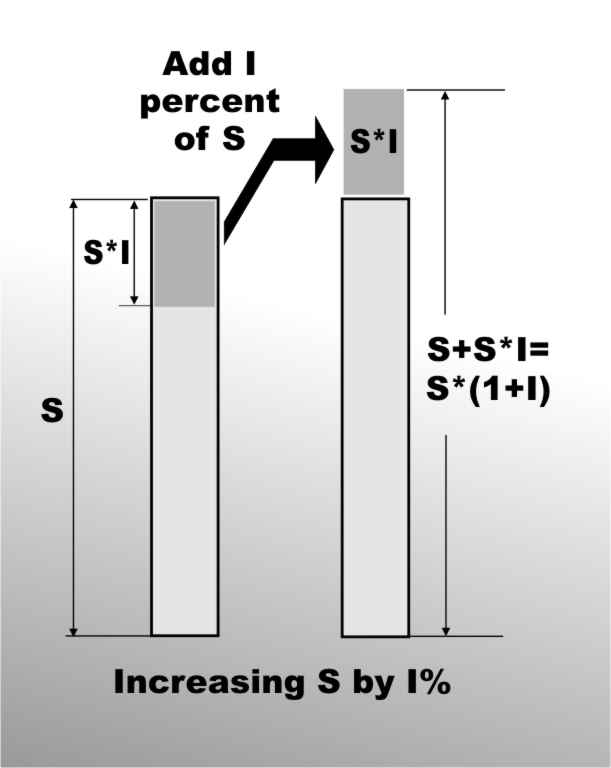
In the remainder of this book we will use the convention that in all formulas percentages are treated as decimal fractions, for example 90% as 0.9 and 5% as 0.05 

Percentage increase/decrease

Working out a simple percentage should cause no one any difficulties given a spreadsheet or even a pocket calculator.

What is slightly more difficult is to work out is the result of increasing or decreasing a value by a given percentage is.

As long as you think about it in the right way even this isn’t difficult. If a value increases by I% then you have the original value plus I% of it where I% is written as a decimal fraction:

value + value *I

or more simply:

value*(1+I)

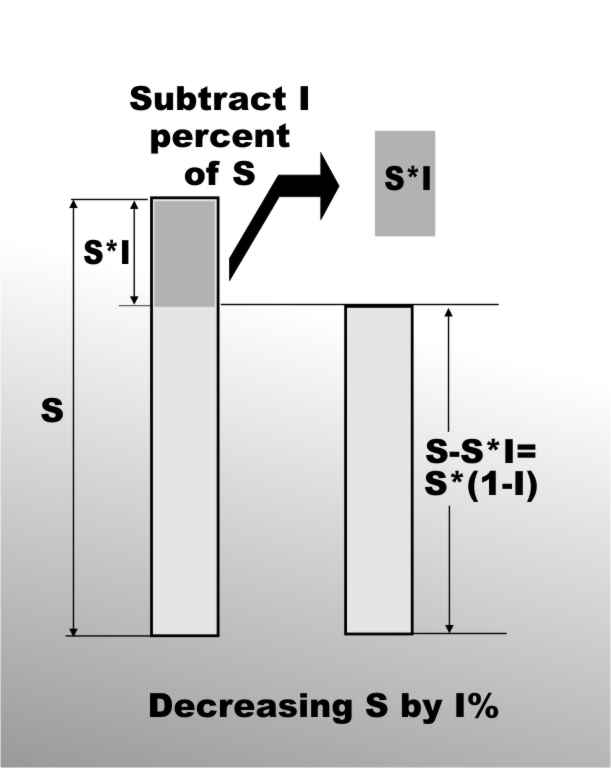
The quantity (1+I) occurs so often in financial functions that it is worth remembering it as what you multiply to increase a given value by I%. In the same way to decrease a given value by I% you multiply by (1-I). 

 Multiplying to increase and decrease by I%

For example, if you are given a 40% discount, that is the price is decreased by 40% of its original value, then the discounted price is given by multiplying by (1-0.4). If you have to pay a 15% surcharge then the surcharged price is found by multiplying by (1+0.15). 

Percentage change at a glance

The use of I, (1+I), (1-I) can be summarized in a table:

Using these formulas you should now find it very easy to work out the effect of a sales tax or value added tax (VAT) on net prices. If the current VAT rate is V% then the gross price can be calculated as:

gross price = Net*(1+V)

Similarly if the discount on a price is D% then the discounted price is given by:

discounted price = price*(1-D)

What percentage change?

Another interesting question is how much percentage increase or decrease has occurred when a quantity changes.

For example, if the price of a product has increased from $2.50 to $3.00 what is the percentage increase. To work this out all you need to do is solve:

new value = old value *(1+I)

for I.

That is, working through the steps needed to get I on its own:

1. Multiply out the bracket
   new value = old value + old value * I


2. Subtract old value from both sides
   new value - old value = old value *I


3. Divide both sides by old value
   (new value -old value)/old value = I

This gives:

I= (new value - old value)/old value

or if you want a more compact version:

I= new value/old value -1

The only change needed for a percentage decrease is to put a minus sign in front of the expression:

I= 1- new value/old value

In the case of the $2.50 to $3.00 increase the percentage increase is 20%, that is:

3.0/2.5-1.0 = 0.2

<ASIN:1118510100>

<ASIN:0735672431>

<ASIN:0789748576>