| Advanced Hashing |
| Written by Mike James | ||||
| Thursday, 22 April 2021 | ||||
Page 2 of 3
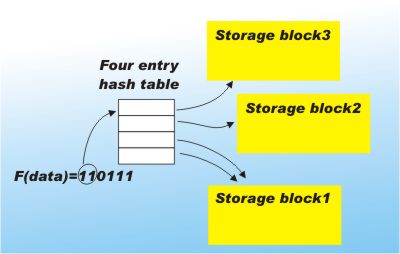
Now consider what happens when one of the blocks becomes full. The obvious thing to do is increase the number of blocks involved in the hashing by increasing the size of the index table. If we use another bit of the hash value the size of the table doubles and it can accommodate twice the total number of blocks. This increasing use of the bits provided by the hash function is what makes the technique extensible. The only problem that remains is that we have to reorganise the existing blocks so that the full blocks are spilt into two new blocks containing the different values of the second bit of the hash value. Each of the full blocks can be split into two blocks by simply using the values of the extra hash bit. That is if the full block held all the data that hashed to 1 say then this block can be split into all the data that hashes to 10 and 11. The nice thing is that we don't have to do anything to the blocks that are not full. The block table can simply map both values of the newly used hash bit to the same block. For example, if the block that holds data hashed to 0 isn't full the table simply maps 00 and 01 to the same block. When a block that has repeated entries in the table finally fills up it can be split in the usual way.
The use of a block table to map the bits of the hash in use to the storage blocks is the key idea. You can reuse blocks until they are full. Blocks only have to be split when they fill up. Of course you still have to search the block for the exact value in which you are interested, but this isn't a serious overhead. If the blocks are arranged to be units of disk storage then you are still guaranteed to access the correct block, i.e. the one that contains the data you are looking for, in a single disk read. Once the block is in memory it can be searched quickly even using a simple linear search. The only real overhead is the need to keep an index table that increases by a power of two each time another bit of the hash value is used to increase the number of blocks, but again a little arithmetic shows that this too isn't a problem as long as the block size is reasonably large. The way that the data is reorganised by splitting blocks is very similar to the way tree structured storage methods such as B trees work. Indeed this approach makes hashing as flexible, more efficient and easier to implement than a B tree index.
<ASIN:0071460519> Functions as tablesThe first step towards perfect hashing is to make a slight change to the way that you think of a hashing function. A function is something that returns a value that depends on an input value. A good hashing function should distribute the key values as evenly as possible though out the hash table. In most cases hash functions are constructed using bitwise logical operators and shift functions in an effort to jumble up the bits that represent the key as much as possible - but there is another way. Instead of using operators to provide the random jumbling why not use a table? Any function can be converted into a lookup table simply by storing its outputs indexed by the input values. As an example consider creating hash function for a single ASCII character. To construct a random hash function using a table all you have to do is set up a 256-element array initialised so that the first element contains 1, the second 2 and so on, i.e.:
The next step is to shuffle the array by moving values randomly around. There are many possible shuffling algorithms but the following is OK:
If you're not too happy about the goodness of the random number generator then do the shuffle more than once. Finally how to use the random table? That's easy - given that the key is just a single character in c, convert it to its ASCII code and look up what is stored in that element of the table i.e.:
As the table has been shuffled the ASCII value is randomly assigned to another value in the range 0 to 255 and this is the result of the hash function. This is fine but only gives us a hash function that will hash a single key made up of a single character. Extending this to a multi-character key isn't at all difficult and just involves finding a way of using the table on each character to build up a final hash value. I'm quite sure that you can think up your own methods but a particularly good one that retains the full benefit of the randomness in the table is:
This takes a random walk around the table starting from h(c) and using the ^ (Exclusive OR) operator to combine the result of the previous step with the ASCII code of the next character. This gives a result in the range 0 to 255 that is very random and depends on all the characters in the string. If you need a second byte for the hash value simply start the random walk again from a different initial point, e.g. by adding one to the initial character's ASCII code. |
||||
| Last Updated ( Thursday, 22 April 2021 ) |