| Data Structures Part II - Stacks And Trees |
| Written by Harry Fairhead & Mike James | ||||
| Friday, 15 October 2021 | ||||
Page 2 of 3
Objects againOf course the modern view isn’t that the stack is a data structure – it’s an object. That is, something with methods, i.e. pop and push, and an existence that goes beyond mere data. If “CStack” is a class based implementation of a stack then in an object-oriented language we can create as many stacks as we like:
These would be used something like:
or
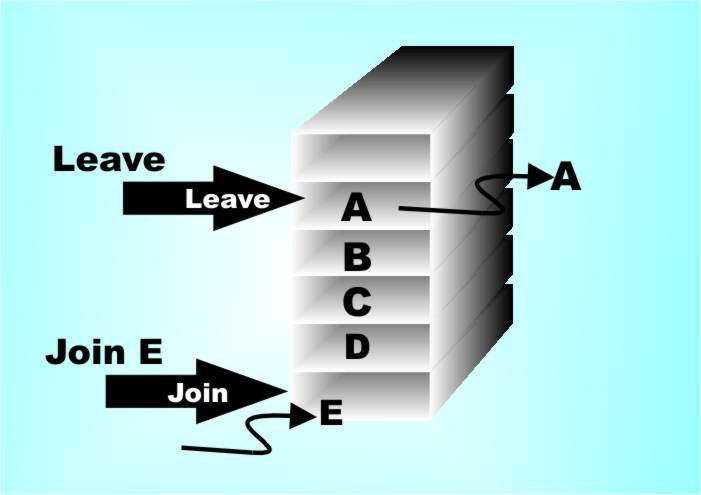
where it is assumed that the methods are push and pop. Notice that the object-based implementation has the advantage that you don’t need to ask how the stack works, what’s inside the object if you like. This means that the programmer can implement the internal working any way that they want and they can even change things without the outside world being any the wiser. Objects are good because they mix the data structure with the code that makes it all work… The Queue & the DequeOnce you have seen a stack you can invent all of the stack-like objects that have ever been thought of, and some. For example, a queue or a First In First Out (FIFO) stack is simply an array with two pointers – one to the start and one to end of the queue. Anything added to the queue goes to the end anything taken from the queue comes from the front. In object-oriented terms the queue has two methods, Join and Leave. A queue doesn’t change the order that things are stored in and it’s mostly useful to slow things down so that they can be processed when the program is ready. (Hardware people often call queues “buffers”.)
A queue has two pointers – one to the start of the queue and one to the end
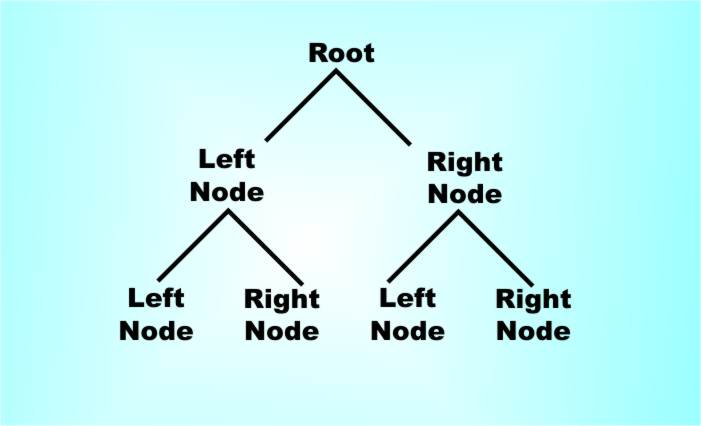
A deque is a queue that you can join and leave from the front or the back and it has four methods, JoinFront, JoinEnd, LeaveFront and LeaveEnd. You are probably getting the idea by now. This sort of data structure simply has methods that adds new things and methods that retrieve new things according to when they were added. For another example a bag is just a data structure that stores data in no particular order. It is typified by an add method and a get or remove method. A bag is different from a set which can only contain one example of each thing you put in it. That is for a bag you can add "A" more than once and how ever many times you added it you can remove it. For a set adding "A" more than once either has no effect or it is an error. In any case the set can only contain one "A". TreesThe tree is probably the most important of the really advanced data structures and in many ways it’s the most complicated and sophisticated. To be abstract for the moment, a tree consists of a set of nodes – the places where the branches do their branching – and the branches that connect the nodes. The idea, or rather the picture, that you should have in your head of a branching tree-like structure is simple enough, actually implementing it in computer terms is not quite as straightforward. To start with the nodes are the things that we work with. A node has space to store the data in the tree, a person’s name for example, and it also stores “pointers” to the nodes that are connected to its child nodes. The big problem is how many pointers? In general a tree can have nodes with as many child nodes as you care to imagine and this is difficult to implement. As a result we like trees that have a fixed number of child nodes – 2 say gives us the binary tree. In this case, i.e. a binary tree, we can refer to the “right child node” and the “left child node” or just the “right” and “left” nodes. A tree also has a first or “root node” that everything else grows from.
In a binary tree each node has two child nodes – one left and one right
Now we can invent an object that behaves like a node in a binary tree, i.e. an object with two properties - left and right child nodes, and a single data property, which stores the value at the node. We can now build a tree by creating a root node:
and then add extra nodes as required:
How do we get at these nodes so that we can grow the tree another level? Easy we just continue the same notation:
and so on. Of course we are also assuming that nodes have a data property which can be used to store whatever you want at each node. For example,
would store the indicated name at the first left child node from the root. You should be able to see how to build up a data structure that corresponds to a family tree in which each “node” gives rise to just two offspring. If you want more, or even a variable number of, offspring at each node then it works in the same sort of way but you need a collection of pointers to the child nodes and this is awkward to write down.
<ASIN:098478280X> <ASIN:0470128704> <ASIN:0201498405> |
||||
| Last Updated ( Friday, 15 October 2021 ) |