| Programmer's Guide To Theory - Gödel And All That |
| Written by Mike James | ||||
| Monday, 16 September 2024 | ||||
Page 2 of 3
The Failure AxiomsWhat could possibly be wrong with this idea? It seems so reasonable that what we know should be extended in this way using nothing but the force of pure logic. There really isn’t any alternative to the idea of logical proof that sane people find acceptable. It also seems entirely reasonable to suppose that applying this method will eventually get us to any statement that is true. What is more, you might as well give a computer the task of shuffling the symbols and seeing what is true. Yes, math is a matter for mechanical computation. Consider now the problems discussed at the start – Fermat’s last theorem and the four-color theorem – their solutions are just a matter of computing time. Now we come to the downfall of the method. You would assume that given a properly formed arrangement of symbols that the computer, or the human, could eventually work out either a proof of the theorem or an anti-proof, i.e. a proof that the negation of the theorem is true thus the theorem is false. It might take a long time, but in principle you could work out if the statement was true or false. This is the assumption of consistency that we suppose will hold for any reasonable or useful system of reasoning.
This sounds so obvious that there is no need to really think about it too deeply, but it is also equally obvious that a statement (let alone a proof or a theorem) has to be either true or false. Now consider: This sentence is false You can begin to see that things are not quite so simple. If the statement is true it is false and if it is false it has to be true. Notice it is self-reference that is causing the problem. This is the paradox of Epimenides (named after the Cretan philosopher Epimenides of Knossos who was alive around 600 BC), and it is the key to Kurt Gödel’s proof that axiomatic systems aren’t consistent in the sense that there are theorems that cannot be proved true or false within the system. There may be a larger system, i.e. one with more axioms in which these theorems are provable, but that’s almost cheating.
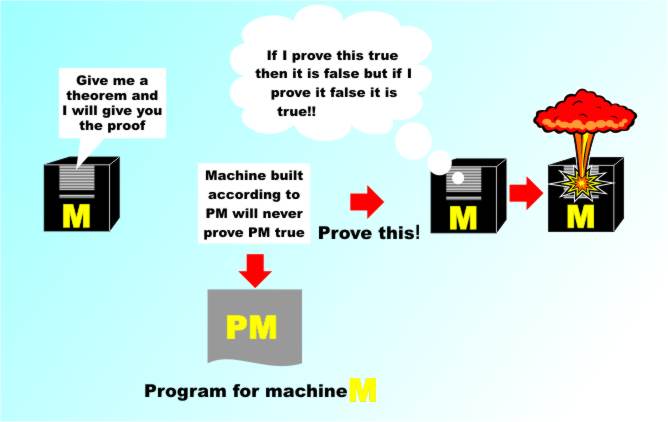
There may be a larger system, i.e. one with more axioms in which these theorems are provable but that’s almost cheating. Gödel’s First Incompleteness TheoremKurt Gödel (1906-1978) The argument that Gödel used is very simple. Let’s suppose that there is a machine M that can do the job we envisaged for a consistent system. That is, the machine can prove or disprove any theorem that we feed to it. It is programmed with the axioms of the system and it can use them to provide proofs. Suppose we ask for the program for the machine written in the same logic used for the theorems that the machine proves. After all, any computer can be reduced to logic and all we are requesting is the logical expression that represents the design of the computer – call this PM for "Program for M". Now we take PM and construct a logical expression, which we’ll call statement X which says: “The machine constructed according to PM will never prove this statement is true” and ask the machine to prove or disprove X. Consider the results. If the machine says “X is true” then X is false. If the machine says “X is false” then Xis true.
The proof that there are theorems that cannot be proved
You see what the problem is here and you can do this sort of trick with any proof machine that is sufficiently powerful to accept its own description as a theorem. Any such machine, and the system of logic on which it is based, must, by its very nature be inconsistent in that there are theorems that can be written using the system that it cannot be used to prove either true or false. In other words there are three types of theorem in the system – those that are provably true, those that are provably false and those that are undecidable using the axioms that we have at our disposal. Is it possible to for a machine to be powerful enough to attempt to prove a statement that involves its own description? Perhaps it is in the nature of machines that they cannot cope with their own description. The really clever part of Gödel’s work was to find that any axiomatic system powerful enough to describe the integers, i.e. powerful enough to describe simple arithmetic, has this property. That is, arithmetic isn’t a consistent axiomatic theory, which means that there are theorems about the integers that have no proof or disproof within the theory of arithmetic. So now think about the 300-year search for a proof for Fermat’s last theorem. Perhaps it wasn’t that the mathematicians weren’t trying hard enough. Perhaps there was no proof. As it turns out we now know that a proof exists, but there was a long time when it was a real possibility that the theorem was undecidable. This example also indicates what to be true but without a proof means. If could be that the axioms of arithmetic are not sufficient to prove some unproven theorem. That is, there is no sequence of steps that take the axioms from their raw form to a proof. However, the theorem may well be true in that there are no integers that satisfy the equation. You cannot even prove it by searching of a counter example because as the search is infinite, you can never conclude that just because you haven’t found a counter example one does not exist. The fact that the theorem is true would just be beyond our reach. You clearly now understand the idea, but do you believe it? To make sure you do consider the following problem: there seem to be lots of paired primes, i.e. primes that differ by two (3,5), (5,7), (11,13) and so on. It is believed that there are an infinite number of such pairs - the so called "twin prime conjecture" but so far no proof. So what are the possibilities? You examine number pairs moving over larger and large integers and occasionally you meet paired primes. Presumably either you keep on meeting them or you there comes a point when you don’t. In other words, the theorem is either true or false. And as it is true or false presumably there should be a proof of this. If you have taken Gödel’s theorem to heart you should know that this doesn’t have to be the case. The integers go on forever and you can’t actually decide the truth of the theorem by looking at the integers. How far do you have to go without seeing a pair of primes to be sure that you aren’t ever going to see another pair? How many pairs do you have to see to know that you are going to keep seeing them? There is no answer to either question. In the same way why do you assume that there is a finite number of steps in a proof that will determine the answer. Why should the infinite be reducible to the finite? Only because we have grown accustomed to mathematics performing this miracle. In the case of the twin prime conjecture recent progress has proved that that are infinitely many primes separated by N and N has to be less than 70 million. This doesn't mean that N is 2 however. Collaborative work by a lot of mathematicians has reduced the upper limit (at the end of 2014) to less than 246 which seems like progress but attempts to reduce if further have not been successful. Can the bound be pushed down as far as 2 or is there really no proof? Repeatedly mathematics proves things using axiomatic logic that otherwise would require an infinite search, but we are not guaranteed that this is possible in all cases. There may well be, and in fact there have to be, cases where no finite proof exists. This is what Gödel’s theorem really is all about. There are statements that are undecidable. If you add additional axioms to the system, the statements that were undecidable might well become decidable but there will still be valid statements that are undecidable in the larger system. Indeed, every time you expand the axioms you increase the number of theorems that are both decidable and undecidable.
|
||||
| Last Updated ( Tuesday, 17 September 2024 ) |