| The McCulloch-Pitts Neuron |
| Written by Mike James | ||||
| Thursday, 04 March 2021 | ||||
Page 2 of 3
More Than Boolean?Given we can make up the basic gates of Boolean logic it is clear that that McCulloch-Pitts networks are up to building anything that can be built with standard logic gates, but are they capable of anything more? The answer is yes and the reason is partly that they have time built into their specification and partly because they are threshold gates. For example, a delay gate can be built using a single excitatory input with a threshold of one. Stacking such gates up provides a delay of more than one time unit. Delaying a signal is the same as remembering it for n time periods, so cells have memory! If you would like a clearer example of the memory inherent in McCulloch-Pitts cells have a look at the following simple latch.
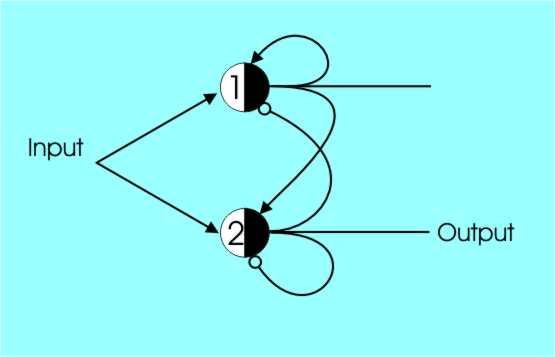
The top cell passes the input to the output if it has a one from the other cell. You can see that the feedback loop in the lower cell keeps it switched on once it is on irrespective of the input on the Start line. Once on the only way to switch it off is to put a one on the Stop line which, being an inhibitor, turns everything off. Divide By TwoIf you know some digital electronics you might well be tempted to try and expand this circuit from a latch to a divide by two circuit – something like a D-Type flipflop. Most people who try come up with a two-cell design something like that shown in the diagram:
A wrong divide by two network
You can see the basic idea. The threshold 2 cell acts as half of a flipflop because of the inhibitory self-feedback. If it is a one it changes back to a zero no matter what the input is. The threshold 1 cell is also inhibited in the same way and every two pulses the whole circuit switches output but there is a problem. If a pulse occurs while the cells are resetting then it is missed completely. In other words, this circuit divides by two but occasionally misses pulses. The correct solution, which doesn’t drop any pulses, needs an extra cell.
The fact that it takes three cells to divide by two is something that surprises many a designer used to standard digital components. What can the brain compute?You can see that it would be possible to continue in this way to build more and more complicated neural circuits using cells. Shift registers are easy, so are half and full adders – give them a try! But at this point you might well be wondering why we are bothering at all? The answer is that back in the early days of AI the McCulloch-Pitts neuron, and its associated mathematics, gave us clear proof that you could do computations with elements that looked like biological neurons. To be more precise, it is relatively easy to show how to construct a network that will recognise or “accept” a regular expression. A regular expression is something that can be made up using simple rules. In terms of production rules any regular expression can be described by a grammar having rules of the type: <non-terminal1> -> symbol <non-terminal2> or <non-terminal1> -> symbol That is, rules are only “triggered” in the right and symbols are only added at the left. For example the rules: 1. <R1>-> A <R2> 2. <R2>-> B<R1> 3. <> -> <R1> are regular. Production rules are used by picking a rule with a left-hand side that matches part of the sequence and then using the right-hand side to re-write that part of the sequence. (The symbol <> means the null sequence, i.e. the sequence with no symbols). Once you see how this works things seem very simple. Starting off from a null sequence <> which matches the lefthandside of Rule 3. The last rule starts things off by allowing use to convert the null sequence <> into <R1> which Rule 1 matches. Rule 1 lets us change <R1> into A<R2> and then rule 2 lets us change this into AB<R1> and so on. You can see that all sequences of the type ABABAB and so on are regular according to this grammar. |
||||
| Last Updated ( Thursday, 04 March 2021 ) |
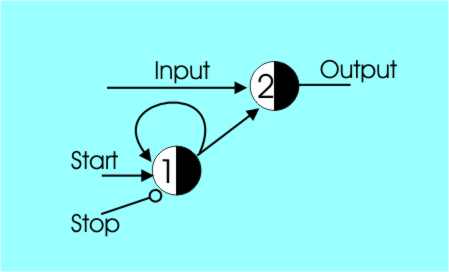 A latch
A latch
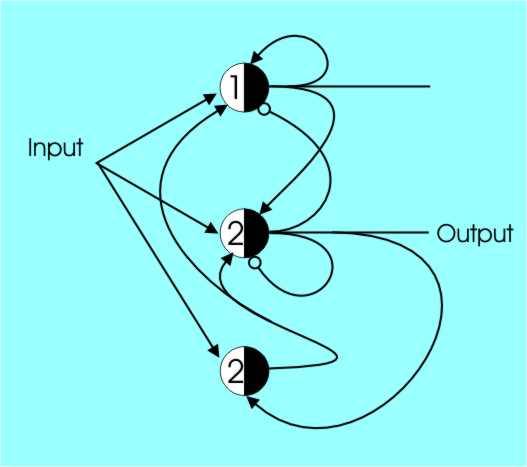 A correct divide by two network
A correct divide by two network