| A Programmer's Guide To Octave |
| Written by Mike James | ||||
| Thursday, 16 March 2017 | ||||
Page 1 of 3 Octave is an open source language, mostly compatible with MatLab, that makes doing difficult math easy. It supports matrix operations and has lots of different types of built-in mathematical operations. It isn't as well known as it deserves to be, and if you are a programmer it can be difficult to find out what you need to know. Hence a programmer's guide.
A Programmers Guide To Languages
Contents
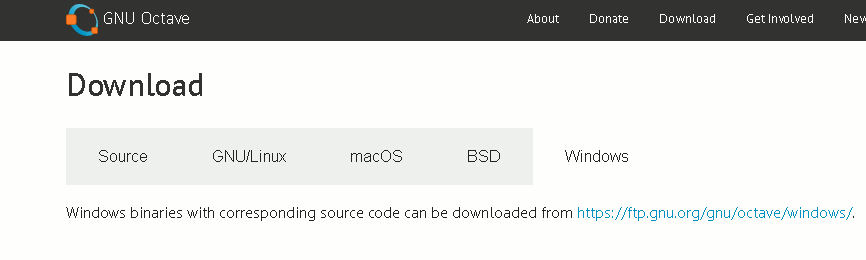
This guide gives you the essence of Octave. It is designed to answer the questions that arise when you first encounter the language with some knowledge of any other language, no matter how slight. It isn't an in depth account and there are lots of topics that aren't even mentioned in passing. The aim is to get you started and to provide an orientation that will make exploring the rest of Octave easier. Octave is an interpreted language that is pragmatic rather than theoretically pure. It gets the job done, but there aren't many interesting language features that are going to make you think hard about programming. However, if you have some math you want to get done, Octave will enable you to solve the problem fast. You can also think of it as the math companion of the R statistical language. Octave is ideal for general math or when you need to implement some general statistical algorithm and play with it. Getting OctaveIf you are running Linux or OSX then you will find binaries for Octave on the Octave site. Windows binaries are a little more difficult. You can install by extracting a compressed file to the correct directories, or you can use the Windows installer version. The Windows installer is easier. All you have to do is visit the Octave site and select Download:
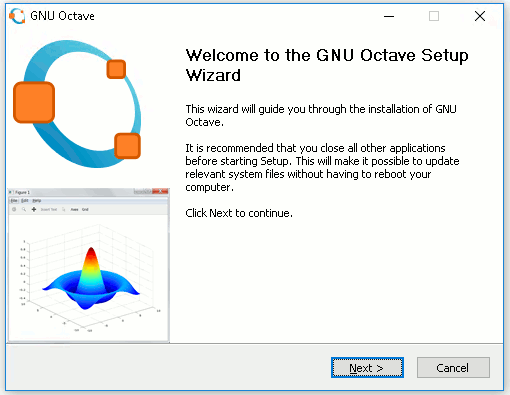
The ftp site is a bit overwhelming at first because it lists all the versions of Octave rather than just the latest. Generally you should pick the most recent version in either 32 or 64 bits depending on the OS you are running. Download the installer and run it:
The installer will guide you through the steps needed to install Octave and you should accept the defaults unlelss you have a good reason not to. At the time of writing you will see a warning that Octave is not supported on Windows 10. Ignore this - it mostly works.
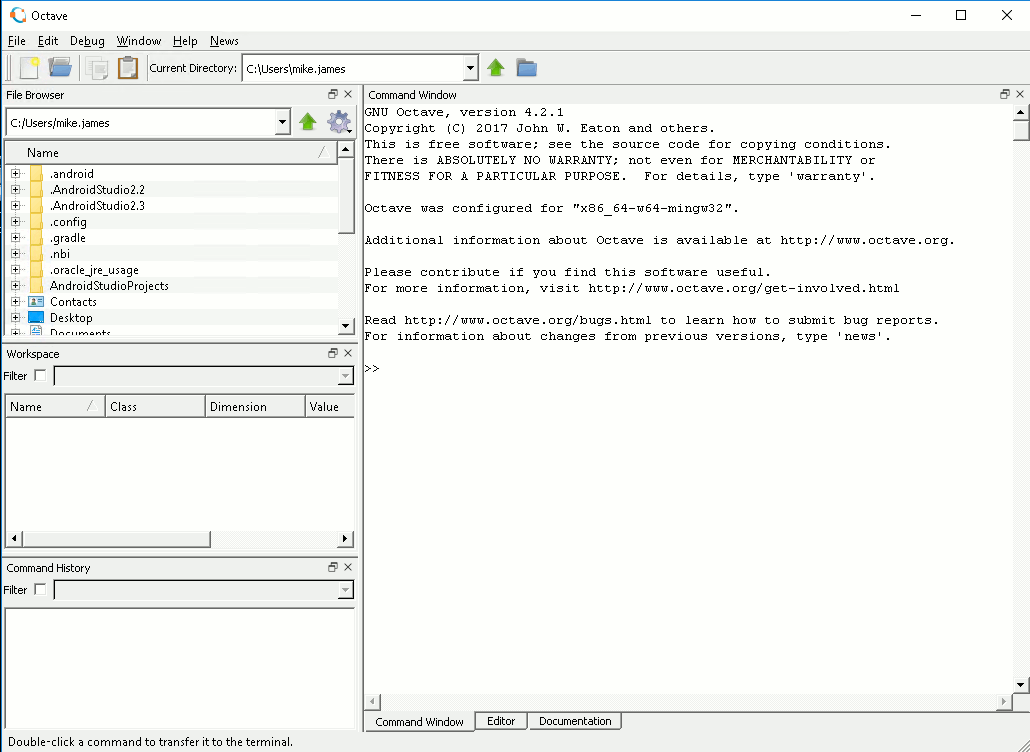
Interactive and PersistentThe latest version of Octave comes with a GUI interface complete with a REPL that allows you to type in commands and see the result at once.
Programming in Octave is slightly different from most languages - as it is a persistent programming environment. What this means is that you work at a command prompt and any variables you create persist for the session. Anything you type is evaluated as soon as you press the return key and the result is displayed - unless you finish the line with a semi-colon when the output is suppressed. That is if you type:
then Octave prints back:
If you later type:
it once again prints:
Once you have created a variable at the command line, it stores whatever value you have given it until you close Octave down or use the clear command. If you type clear then all variables are removed from the environment and if you then type A you will see the error message "error 'A' undefined near line x column y" This retained or persistent mode is great for interactive programming. For example, you can read or type in a data matrix and then try out commands to compute whatever you are trying to get from it. This is a good way to learn Octave but at some point you will want to write something that looks more like a traditional program that you load and run. This is very easy but it is important to realize that this all works within the persistent environment and code that you read in from a file is treated just like code you type in. That is after the code has run the environment has changed according to what variables the code created and modified. This means you can work by running one program on some data you typed in and then run another program to process the results of the first program. If this very interactive style of working worries you - don't fret because you can create programs that work in isolation simply by starting them off with the clear command. ProgramsSo how do you create an Octave program? The answer is you can simply put the code that you would have typed at the command line into a file with a name that ends in .m. The GUI interface comes with an editor but you can use any editor you care to but NotePad or NotePad++ are good choices. You can invoke the editor within Octave by typing edit filename which editor you get depends on the system and how it has been configured. If you don't change the default configuration then you will get the built in GUI editor which is what I recommend using to get started at least. To run an Octave program you can simply type its name at the command prompt. Of course the file has to be stored in the current directory and you need to know that the ls command will list the contents of the current directory and the cd will change the directory in the usual way. If you have created a program in a file and when you type the name Octave cannot find it and reports an "undefined" error then it is most likely that the file isn't in the current directory. The new GUI editor provides features such as syntax highlighting and you can use it to directly run a program and even set breakpoints for debugging. So for example if you start the editor using File,New, New Script and enter the commands:
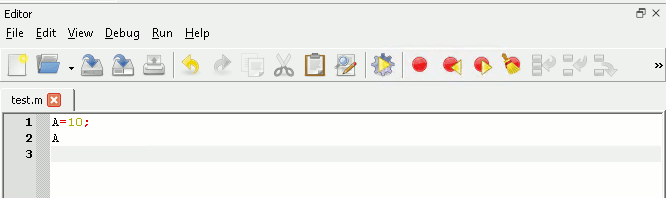
You can run it by clicking on the Save and Run icon - the gear wheel with the arrow - give the file the name Test. The only question is where is the output? The answer is in the command Window which you can switch to using the tabs at the bottom of the screen. A better idea is to drag the command Window to a new location and tile it so that you can see it and the editor. When you do see the command window you will see displayed:
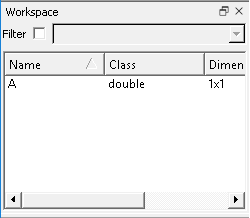
Notice that after the program has run, A is still defined and has the value 10 so you can carry on using it by typing in commands at the command prompt or by running other programs that use a variable called A. You can see what variables have been defined in the Workspace window along with information about their type:
Also notice that Octave is case sensitive, so if you saved the file as "Test.m" you have to type "Test" whenever yopu want it; "test", "TEST", "tesT" or any other variation just doesn't work. If the file contains a function - see later - then you can call the function just by typing the file name followed by brackets and any arguments. For example if Test.m contains a function you can write Test() to run the function. <ASIN:1849513325> |
||||
| Last Updated ( Thursday, 12 October 2017 ) |