| Hyperbolic Maps Save the Internet |
| Monday, 13 September 2010 | |||
|
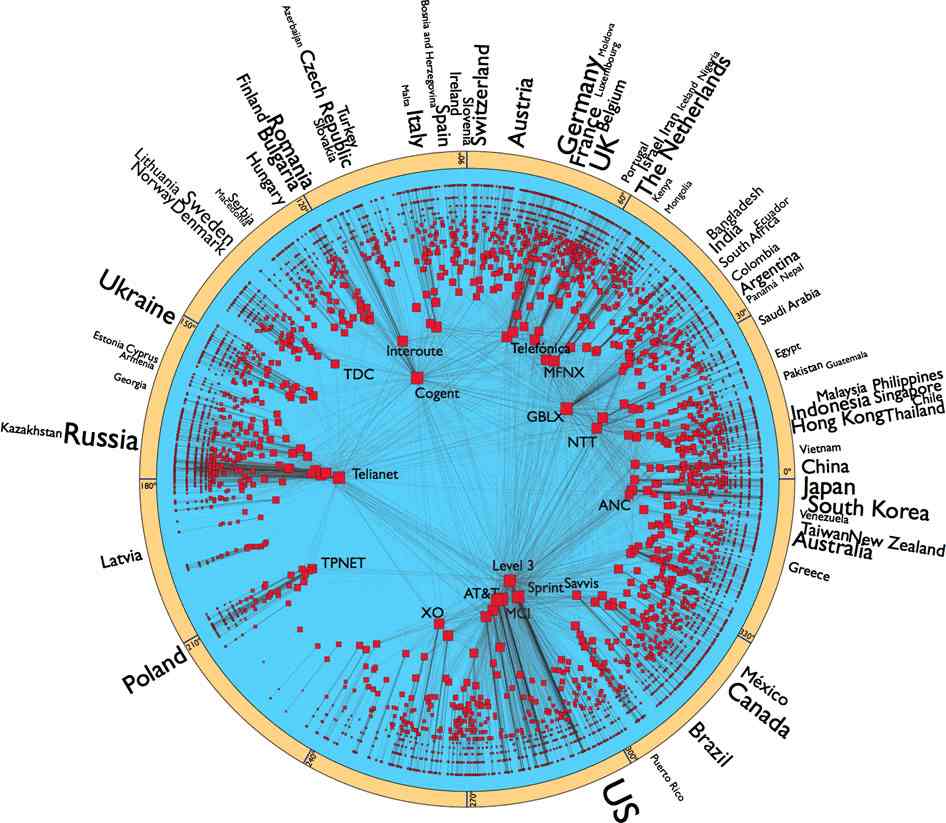
Can a hyperbolic map save the Internet from falling into a black hole? It's all a matter of applying greedy routing algorithms and having a good map.
The Internet is a wonderful creation and no one person can take the credit - it sort of just grows. The connections between different portions of the net are made for reasons other than an overall global plan - in fact there is no global plan. When you send a packet off onto the wires it gets routed to its destination by a fairly simple algorithm that mostly seems to work. Yet as the Internet gets bigger there is the question of whether or not it will continue to work. This is something that is starting to worry people an now we have a plan that might stop the whole thing falling over - and it's not a global plan. Three researchers Marián Boguñá,Fragkiskos Papadopoulos & Dmitri Krioukov have put forward a theory of how the Internet is actually connected in order to stabilise it: "The constantly increasing size and dynamics of the Internet thus leads to immense and quickly growing routing overheads, causing concerns among Internet experts that the existing Internet routing architecture may not sustain even another decade; parts of the Internet have started sinking into black holes already" Currently the routing algorithm uses pure topology, i.e. what is connected to what, to route packets. Each router keeps a list of paths to use to pass a packet to an increasingly more specific location. This requires a lot of organisation and a lot of data to be transferred between routers. What the research team and others have long realised is that a more intelligent "greedy" store-and-forward system could be made to work. A good way to think of this is to imagine trying to navigate from town A to town B using nothing but a map that gives all of the connections between A and B. This works well as long as the list is up-date and correct. If a connection is broken at one point then to get from A to B would need a complete topological map update to be transmitted to A. Now consider how you actually get from A to B in the real world. In the real world your map shows distances and the direction that B is in. You could get to B without having to work out a complete route simply by moving to the next town that is closer to B. At each move you could pick the road that gets you maximally closer to B in that step - it is in this sense that the routing algorithm is greedy. At the moment routing algorithms are topological but to make them greedy we need some geometry - specifically a measure of distance or a metric. This is what the latest research is all about. After analysing the net, the group has found that using a hyperbolic metric is efficient. A hyperbolic metric crams more and more space into the "universe" as you move closer to its edge. So a hyperbolic 2D universe in the form of a circle has most of its area near to the edge of the circle. In fact the growth factor is exponential.The 2D hyperbolic representation is called a Poincaré disk and it's a favourite device in the drawings of M C Esher.
The use of a hyperbolic space makes sense for the Internet because the space needed to hold the huge number of smaller networks is much greater than that needed for the relatively fewer big networks. To use the hyperbolic map routers would simply determine the direction of the destination and pass the packet to the node that was in that direction, moving as close as possible in the hyperbolic metric to the destination in one step.
Would it work in reality? At the moment all we have are simulation results that show that it works well. There is no proof of optimality and it seems unreasonable to expect any. The authors conclude: We have shown that the Internet hyperbolic map is remarkably robust with respect to even substantial perturbations of the Internet topology, implying that this map is essentially static. It does not significantly depend on topology dynamics, You can read the full paper at: Sustaining the Internet with hyperbolic mapping
<ASIN:3836503182> <ASIN:3822837032> <ASIN:0810981130> <ASIN:0810922681> <ASIN:0810924145> |
|||
| Last Updated ( Monday, 13 September 2010 ) |