| More Ties Than We Thought Or Ties Of The Matrix |
| Written by Lucy Black |
| Wednesday, 26 March 2014 |
|
The Matrix Reloaded started something when "The Merovingian" wore a number of very flashy ties. The problem was that we thought we knew how many ways you can tie a tie, but the enumeration didn't include the Matrix way of doing it. Now we know how many knots there are and it's all thanks to language theory. The number of ways you can tie a tie had been enumerated in 2001 and the answer was that there were exactly 85 different ways. When the Matrix Reloaded hit the silver screen the whole theory had to be rethought because the character known as the "Merovingian" was wearing his tie in a new way that stirred up enough interest for people to spend time working out how it was tied.
A close up of the tie in question - it's black on black so difficult to see exactly how the knot works.
As a result a whole set of knots were invented that all used the novel approach of tying the tie using the thin end - the thin blade - of the tie. Doing this allow a range of "textured" knots that some people find attractive. The original 85 knots were restricted to having smooth front faces.
Three tie knots - two classics, the 4-in-hand and the double windsor plus a modern knot with a textured facade - the trinity.
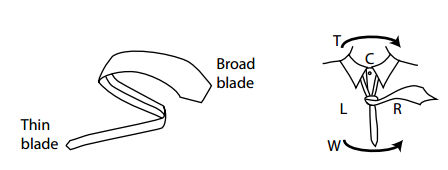
So how many "Merovingian" knots are there? The question is answered in a new paper "More ties than we thought", by Dan Hirsch, Meredith L. Patterson, Anders Sandberg and Mikael Vejdemo-Johansson. The methodology is based on the original enumeration and an interesting application of language theory. The idea is to create a programming language for tying ties. The parts of a tie and the division of the wearer's torso and winding directions can be seen in the diagram taken from the paper:
which gives the sequence of moves of the end of the tie in relation to the divisions of the torso and the direction of the move - towards or away from the body. Thus each knot corresponds to a sequence of symbols like RCLCRC and so on. Of course, some moves are impossible and you need a set or rules to restrict the sequences to only those that are possible. In other words you need a grammar for the legal symbol strings that correspond to physically possible tyings. This is where the language theory comes into the picture. If the you focus only on single depth tie knots, i.e. only tucking the active blade under the most recent bow, then the grammar is regular. The class of the language for deeper tuckings isn't currently known, but it has to at least context-free. The next step is to ask what the size of the language generated by the grammar is. For single depth tucks there are 177147 different sequences and hence knots. Of these there are 2046 winding patterns that take up to 11 moves, the same as the The Merovingian knot and other popular knots, and so these are probably practical with a normal length necktie.
As always there are some open questions. What is the complexity class of the full language? How can the grammar be modified to account for different knot facades and hence obtain a classification all possible knot facades. Who would have thought a little movie would have attracted so much attention....
More InformationMore ties than we thought (pdf) Related ArticlesSix Degrees Of Separation Is New Pancake flipping is hard - NP hard
To be informed about new articles on I Programmer, install the I Programmer Toolbar, subscribe to the RSS feed, follow us on, Twitter, Facebook, Google+ or Linkedin, or sign up for our weekly newsletter.
Comments
or email your comment to: comments@i-programmer.info
|
| Last Updated ( Monday, 07 April 2014 ) |