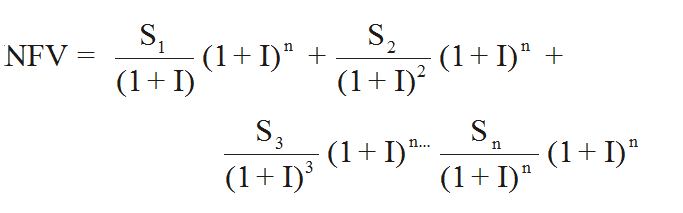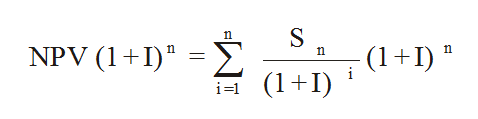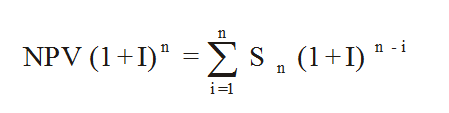The only question is what interest rate is appropriate.

You might think that as the rate is 6% per annum the appropriate rate for a half yearly cashflow is 6%/2.

This isn’t the case because it doesn’t take into account the different compounding periods.

The correct interest rate to use is the effective interest rate calculated from the annual rate. As explained in Chapter 3,  the effective rate gives you an interest rate that can be applied over a different compounding period while still giving the same result as the original rate. The formula relating the two is simply

 effective=(1+I)^m-1

where m is the new compounding period measured in units of the original period. In this case m=.5 and the formula for the effective rate is:

 (1+B1)^.5-1

which should be entered into B2. Now the NPV formula can be entered into B10:

 NPV(B2,B4..B9)

and you can see that the result is the same as the first calculation.

Whenever you alter the period of an NPV calculation you must make sure that the interest rate that you are using is the appropriate one. As the NPV calculation is based on compound interest rates should be converted using the nominal to effective formula.

Net Future Value

In the same way that we can define the Net Present Value or an irregular cashflow we can define the Net Future Value

Each of the terms in the cashflow is multiplied by (1+I)^m where m is the number of periods from the end of the loan that the payment is received.

That is if $Si is received at the end of period i then:

NFV= S1(1+I)^n-1+S2(1+I)^n-2+
                      S3(1+I)^n-3....Sn

You can see that the NFV is just the amount that you would accumulate if you invested each of the cash sums as soon as it was received at I% for the remainder of the term of the investment.

In more mathematical terms the NFV is:

For example, if an investment promises to generate a cashflow of $100 at the end of the first year, $200 at the end of the second and $500 as a closing payment then the Net Future Value is:

 NFV=100*(1+I)^2+200*(1+I)^1+500

where I is the effective annual rate of interest.

If I is assumed to be 8% then the NFV is $832.64 which should be compared to the total income of $800 and the NPV of $660.98. You should be able to see from this example that the NFV really is just the amount you accumulate by investing each of the cashflows as they arrive.

The NPV-NFV relationship

For each cash sum in the cashflow the NPV discounts it back to what would have to be invested to produce the sum and the NFV compounds it forward to what it would produce if invested immediately it is received.

There is a very simple and general relationship between NPV and NFV:

 NFV=NPV*(1+I)^n

In other words, if you invest the NPV for n years at I% the final sum is the NFV.

To see that this is true, skip this section if you are happy to take it all on trust, all we need to do is return to the general formula of the NPV and multiply it by (1+I)^n:

If you multiply though by (1+I)n you get:

which when you cancel the (1+I)^i factor on the bottom of each term from the (1+I)^n factor gives:

which is of course the definition of the NFV given earlier.

Hence the NFV really does always equal the NPV multiplied by (1+I)^n.

In more mathematical terms what we have just shown can be written as:

and cancelling out the (1+I)^i with the (1+I)^n gives:

and you should once again recognise the right-hand side as being the definition of the NFV.

Because of this simple relationship there is no need for an NFV financial function. In all cases you can use

NFV=NPV(I,range)*(1+I)^n

where n is the number of cashflows.

Notice that all of this still assumes that the cashflows occur at the end of each period. If this is not the case then slight modifications have to be made but the general principles remain unchanged and the relationship between the two values still holds.