|
Page 1 of 2 This xkcd cartoon provides an ideal excuse to explain Kolmogorov complexity. It is an interesting topic and one that gets right to the heart of programming of how programming relates to ideas like information and entropy. This is a subject that still has lots of mysterious connections with things outside of computing.
Kolmogorov Directions

More cartoon fun at xkcd a webcomic of romance,sarcasm, math, and language
A Programmers Guide To Theory
First Draft
There is a more recent version of this:
Now available as a paperback and ebook from Amazon.

Contents
- What Is Computable?
- Finite State Machines
- What is a Turing Machine?
- Computational Complexity
- Non-computable numbers
- The Transfinite
- Axiom Of Choice
- Lambda Calculus
- Grammar and Torture
- Reverse Polish Notation - RPN
- Introduction to Boolean Logic
- Confronting The Unprovable - Gödel And All That
- The Programmer's Guide to Fractals
- The Programmer's Guide to Chaos*
- Prime Numbers And Primality Testing
- Cellular Automata - The How and Why
- Information Theory
- Coding Theory
- Kolmogorov Complexity
*To be revised
Suppose I give you a string like 111111... which goes on for say one hundred ones in the same way. The length of the string is 100 characters but you can write a short program that generates it very easily -
repeat 100
print "1"
end repeat
Now consider the string "231048322087232.." and so on for one hundred digits. This is supposed to be a random string, it isn't because I typed in by hitting number keys as best I could, but even so you would be hard pressed to create a program that could print it that was shorter than it is.
In other words, there is no way to specify this random-looking string other than to quote it.
This observation of the difference between these two strings is what leads to the idea of Kolmogorov complexity.
The first string can be generated by a program with roughly 30 characters, and so you could say it has 30 bytes of information, but the second string needs a program of at least the hundred characters to quote the number as a literal and so it has 100 bytes of information.
You can already see that this is a nice idea but it has problems. Clearly the number of bytes needed for a program that prints one hundred ones isn't a well-defined number - it depends on the programming language you use. However, in any programming language we can define the Kolomogorov complexity as the length of the smallest program that generates the string in question.
So complexity is defined with respect to a given description language.
For infinite strings things are a little more interesting because, if you don't have a program that will generate the string, you essentially don't have the string in any practical sense.
That is, without a program that generates the digits of an infinite sequence you can't actually define the string.
This is also the connection between irrational numbers and non-computable numbers.
An irrational number is an infinite sequence of digits.
For example:
2.31048322087232 ...
where the ... means carry on forever.
Some irrationals have programs that generate them and as such their Kolmogorov complexity is a lot less than infinity.
However, as there are only a countable number of programs and there are an uncountable number of irrationals (see The Programmer's Guide To The Transfinite) there has to be a lot of irrational numbers that don't have programs that generate them and hence that have an infinite Kolmogorov complexity.
Put simply, there aren't enough programs to compute all of the irrationals.
This also means that there are an infinite number of irrationals that have infinite Kolmogorov complexity.
To be precise there is an Aleph zero or a countable infinity of irrational numbers that have Kolmogorov complexity less than infinity and an Aleph one or an uncountable infinity of them that have a Kolmogorov complexity of infinity.
The ones that have a smaller than infinite Kolmogorov complexity are very, very special but there ar an infinity of these too. In a sense these are the "nice" irrationals - numbers like π and e that have interesting programs that compute them to any desired precision.
How would you count the ones that had a less than infinite Kolmogorov complexity?
Simple just enumerate all of the programs you can create by listing their machine code as a binary number. Not all of these programs would generate a number, indeed most of them wouldn't do anything useful but among this Aleph zero of programs you would find the Aleph zero of "nice" irrational numbers.
Notice that included among the nice irrationals are some transcendental. A transcendental is a number that isn't the root of any polynomial equation. Clearly is a number is the root of a finite polynomial, i.e. not transcendental but algebraic, you can specify it by writing a program that solves the polynomial. For example, the square root of 2 is an irrational but it is algebraic and so it has a program that generates it and hence its a nice irrational.
Kolomogorov Complexity Isn't Computable
The second difficulty inherent in the measure of Kolmogorov complexity is that given a random-looking string you can't really be sure that there isn't a simple program that generates it. This situation is slightly worse than it seems because you can prove that the Kolmogorov complexity of a string is itself a non-computable function.
That is, there is no program (or function) that can take a string and output its Kolmogorov complexity. The proof of this is essentially in the long tradition of such non-computable proofs, i.e. proof by contradiction.
If you assume that you have a program that will work out the Kolmogorov complexity of any old string then you can use this to generate the string using a smaller program and hence you get a contradiction.
However, this isn't to say that all is lost.
You can estimate the Kolmogorov complexity for any string fairly easily. If a string is of length L and you run it through a compression algorithm you get a representation which is L-C in length where C is the number of characters removed in the compression. You can see that this compression factor is related to the length of a program that generates the string, i.e. you can generate the string from a description that is only L-C characters plus the decompression program.
Any string which cannot be compressed by even one character is called incompressible. There have to be incompressible strings because, by another counting argument, there are 2n strings of length n but only 2n-1 strings of length less than n.
That is, there aren't enough shorter strings to represent all of the strings of length n.
Again we can go further and prove that most strings aren't significantly compressible, i.e. the majority of strings have a high Kolomogorov complexity. The theory says that if you pick a string of length n at random then the probably that it is compressible by c is given by 1-21-c+2-n.
Plotting the probability of compressing a string by c characters for a string length of 50 you can see at once that most strings are fairly incompressible once you reach a C of about 5.
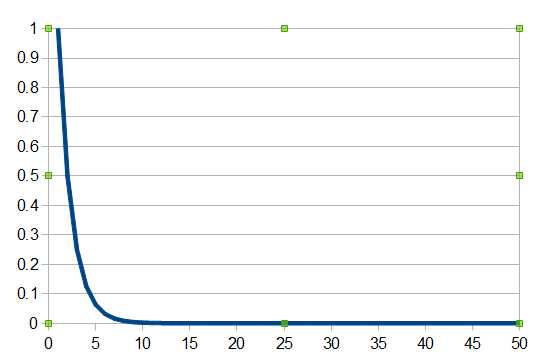
Armed with all of these ideas you can see that a string is algorithmically random if there is no program shorter than it that can generate it - and most strings are algorithmically random.
If complexity is related to randomness then it should also be connected to entropy. If you use a Markov source to generate strings then their complexity divided by their length converges in a reasonable sense to the entropy of the source.

|


