Algorithms 

Algorithms for working with floating point numbers are very complex and very easy to get wrong.

Early computers, or perhaps it should be early programmers, suffered a lot from poor floating point implementations. Often values that floating point routines produce are closer to random numbers than true values.

For example, consider the algorithm for adding two floating point numbers.

You can’t simply add the fractional parts because the numbers could be very different in size. The first task is to shift the fraction with the smallest exponent to the right to make the two exponents equal.

When this has been done the fractional parts can be added in the usual way and the result can then be normalised so that the fraction is just less than one.

Sounds innocent enough but consider what happens when you try to add 1 x 2^-8 to 1 x 2⁸ using an eight-bit fractional part. Both number are represented in floating point form as 0.1 but with exponents of 2^-7 and 2⁹ respectively.

When you try to add these two values the first has to be shifted to the right nine times with the result that the single non-zero bit finally falls off the end and the result is zero in the standard precision. So when you think you are adding as small value to 1 x 2⁸ you are in fact adding zero.

Not much of a problem but try the following program in C# (the same would happen in most languages only the values used would change):

  float v = 0.999999F;
  do
  {
    v = v + 0.0000001F;
  } while (v<1);

This program does complete the loop but if you add one more zero before the 1 in the quantity added to v, the loop never ends.

Floating point arithmetic can be dangerous!

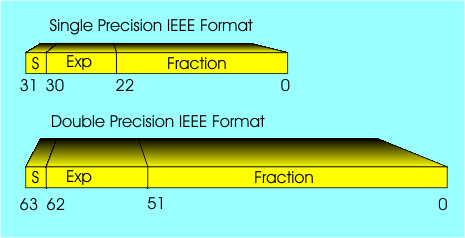
IEEE standard

To try to make it safer there is a standard for floating point arithmetic, the IEEE standard, which is used by nearly all floating point hardware, including all flavours Intel derived hardware since the Pentium was introduced.

Single precision IEEE numbers are 32 bits long and use 1 sign bit, an 8-bit exponent with a bias of 127 and a 23-bit fraction with the first bit taken as a 1 by default. This gives 24 bits of precision and you should now see why the  loop listed above fails to operate at exactly 7 zeros before the 1.

Similar problems arise if you try other arithmetic operations or comparisons between floating point values that are on very different scales.

The IEEE standard floating point formats are used inside nearly every modern machine.

It isn't so long ago that floating point hardware was an optional extra. Even quite sophisticated microprocessors such as the 486 lacked the hardware. You could buy add-on numeric coprocessors which were microprocessors that were optimized for doing floating point arithmetic. From the software point of view not knowing if floating point arithmetic was going to be provided by a library or hardware was a big problem and it stopped early desktop microcomputers doing some types of work.

Early numeric coprocessors didn't always get the algorithms right and they weren't necessarily based on the IEEE standard. There have even been failures to implement the hardware that computes with numbers in the IEEE standard but today things have mostly settled down and we regard floating point arithmetic as being available on every machine as standard and as being reliable.

The exception, of course, are the small micro-controller devices of the sort that are used in the Arduino, say. When you come to program any of these integer arithmetic and hence fixed point arithmetic is what you have to use. The only alternative is to use a software based floating point library which is usually slow and takes too much memory.

So the art of fixed point arithmetic is still with us and you do need to know about binary fractions.

Related Articles

Binary Arithmetic

Binary - negative numbers

Andrew Booth and the ARC

Pre-history of computing

What Programmers Know

Contents

1. The Computer - What's The Big Idea?*
2. The Memory Principle - Computer Memory and Pigeonholes*
3. Principles of Execution - The CPU
4. Assemblers and assembly language*
5. The Essence Of Programming
6. Variables - Scope, Lifetime And More*
7. Binary Arithmetic
8. Hexadecimal*
9. Binary - Negative Numbers*
10. Floating Point Numbers*
11. Inside the Computer - Addressing
12. The Mod Function
13. Recursion
14. The Lost Art Of The Storage Mapping Function *
15. Hashing - The Greatest Idea In Programming
16. Advanced Hashing
17. XOR - The Magic Swap*
18. Programmer's Introduction to XML
19. From Data To Objects*
20. What Exactly Is A First Class Function - And Why You Should Care*
21. Stacks And Trees*
22. The LIFO Stack - A Gentle Guide*
23. Data Structures - Trees
24. Inside Random Numbers
25. The Monte Carlo Method
26. Cache Memory And The Caching Principle
27. Data Compression The Dictionary Way
28. Dates Are Difficult*
29. Sequential Storage*
30. Magic of Merging*
31. Power of Operators
32. The Heart Of A Compiler*
33. The Fundamentals of Pointers
34. Functional And Dysfunctional Programming*

* Recently revised

Comments

Make a Comment or View Existing Comments Using Disqus

or email your comment to: comments@i-programmer.info

To be informed about new articles on I Programmer, sign up for our weekly newsletter, subscribe to the RSS feed and follow us on Twitter, Facebook or Linkedin.

<ASIN:1871962439> 

<ASIN:1871962722> 

<ASIN:1871962714>

<ASIN:1871962420>