| How To Number Crunch - NAG for .NET |
| Written by Mike James | |||
| Wednesday, 08 June 2011 | |||
|
Number crunching in C# (or any .NET language) is a problem because it doesn't have a long tradition of implementing numerical methods. So why not use a library that was originally implemented in Fortran, the language of choice, when you want to work something out?
Yes I know the temptation is to always do it yourself. You have the paper that describes the method so why not just implement it from scratch? After all it can't take long as numerical programs are never complicated or run to many lines. Yes, I have done it myself and well remember the hours of work spent testing and finding the bugs in my principle components (eigenvalue) routine and at the end of the day did I really trust it? No not really. The problem with numerical methods is that even if you understand the theory actually implementing the calculation is usually not as simple as writing down the theory in code. You have to take account of the extreme cases, consider accuracy and stability. You also have to test in ways that normal software just isn't subjected to and you have to know the limits of the methods and implementations. So it is much easier to get some well trusted off the shelf solution. But... it's then a matter of figuring out how it all works. NAG Library for .NETFor a recent project I decided to try The Numerical Algorithms Group's NAG Library for .NET. The reason for the choice is that the NAG Library has been round almost as long as I can remember and for this reason alone it is worthy of your trust. It can be used from C#, VB, C++ or F# and it works in a 32-bit or 64-bit environment. The .NET library takes the form of managed wrappers around the Fortran library. Before you worry about not using a 100% native managed approach think how much better it is to have the security and robustness of the original Fortran library. You can't code a new library from scratch, even with the model of something that works in front of you, and not expect to put some bugs in. The library includes routines for:
It is important to stress that each category includes multiple methods and there are over 200 methods in total. Getting started with NAGTo use the NAG Library for .NET all you have to do is to install it, start a new C# project in Visual Studio and add a reference to the DLL - Naglibrary32 or Naglibrary64 and add: using NagLibrary; Before you do start to make use of it, though, you probably need to use the example program included in the install. This isn't really an example more a verification application. You can run any of the methods in the library simply by selecting it and then you can compare the output with that produced by a reference installation. This is a good way to pick up any problems before they find their way into your code. It seems like a good idea to check any routine in this way before you start using it and it provides a good way to determine that updates haven't broken the system while you weren't looking. So how do you use the numerical method of your choice? The first thing to say is that you won't find a method called eigenvectors or anything human readable. All of the methods are grouped together into families of similar types indicated by a three character name. So G03 is multivariate methods, G05 is random number generators and so on. Each three letter family has been implemented as a static class with methods that correspond to each of the numerical techniques in the family. For example the static class X01 includes x01aa and X01ab which give the constants pi and gamma respectively. So to get pi into a double you would use: double NagPi = X01.x01aa(); It is true that at first the use of a systematic but not meaningful naming system seems very strange but you soon find the routines you want to use and it has the advantage that variations and related methods are close by in the naming structure. There is also the very useful intellisense prompting which gives you not only the possible methods you could use but a short description of what they do.
Random Number GeneratorLet's look at a slightly more involved example - a random number generator. The library has lots of different types of random number generator but let's do something simple and generate an array of ten random numbers. First we need to create a state object which is used to control how the base random number generators are set up. int fail=0; The first two parameters set the generator type. In this case it sets up the NAG basic generator (a standard congruential generator) . The seed sets the initial values for the generator - different generators need different numbers of seeds but the basic generator only needs one. The fail variable is used to signal an error and we should really test that it is zero i.e. no error before continuing. Once the state object is setup we can obtain a vector - in this case of ten random values: int n = 10; The random values are in the range 0 to 1 and are returned in x. Notice that fail is used to indicate an error and again we should test it before moving on. As a slightly more complex example let's generate a random orthogonal matrix - a task that is more difficult than you might think at first statement. The task might be difficult but the way that you use the library is simple enough. You need a status object to initialize the random number generator as before and an array to hold the result: double[,] matrix = new double[n, n]; The method has a number of parameters that make it more useful. You can opt for the generated matrix to multiply the supplied matrix on the left or right using the first parameter or you can set it to be initialized to the identity using the second. To test that we really do have an orthogonal matrix we can multiple it by its transpose and expect to see the identity. To do this we make use of a method that forms the expression: aAB+bC where A,B and C are matrices and a and b are scalars. Either of the matrices can also be transposed in the operation. For example, to form AAT you would use: double[,] resultMatrix = new double[n, n]; where the first two parameters specify that the first matrix is to be left alone and the second transposed. As we only want to multiply two matrices a is set to 1 and b set to zero - the result is returned in the third matrix i.e. resultMatrix and any errors are reported using fail.
Reliable Number CrunchingSo that's all there is to using the NAG library for .NET. As the actual number crunching code is compiled from the original Fortran library you can be sure that once the transfer is made from the .NET language of your choice to one of the methods then it will be as efficient, robust and correct as possible. It will certainly be more efficient that the equivalent method implemented in C# say. The use of static methods to wrap the numerical methods seems like the best way to do the job. Where needed the library does make use of .NET mechanisms to get things done - for example delegates are used to pass evaluation functions. Getting to know the library is a matter of looking in the class of routines that you are interested in and working through what methods are provided. Even though the examples given earlier are focused on using random number generators and matrices the general principles are the same for the majority of the methods. For more information visit: NAG Library for .NET
If you would like to be informed about new articles on I Programmer you can either follow us on Twitter or Facebook or you can subscribe to our weekly newsletter.
<ASIN:1449380344> <ASIN:0123745144> <ASIN:0321658701> <ASIN:0321741765>
|
|||
| Last Updated ( Sunday, 26 March 2017 ) |
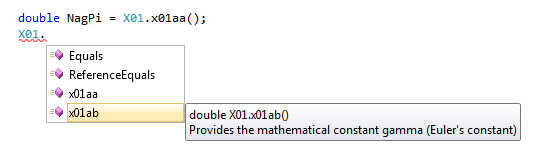
 Online help - click to enlarge
Online help - click to enlarge