| Find N-Body Solutions In Your Browser |
| Written by Mike James |
| Sunday, 11 January 2015 |
|
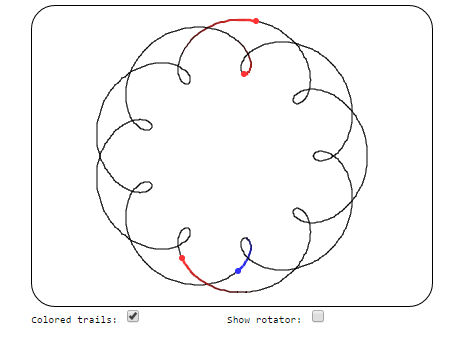
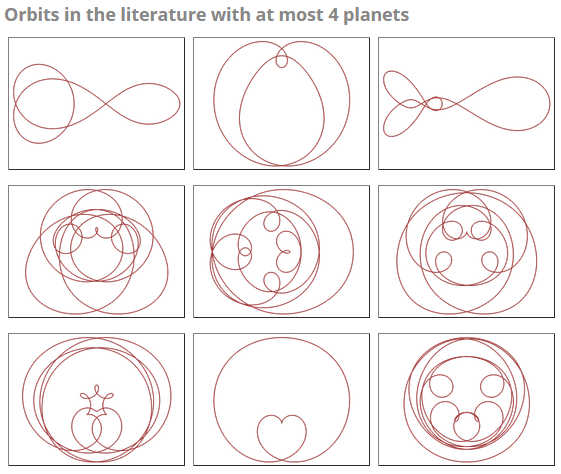
When three or more bodies, planets say, move under their own gravity they can produce amazing orbital patterns. With Choreo.2.3.js you can try your hand at finding new solutions interactively in a browser. If you did any physics, you might know that two-body problems are mostly easy but three-body problems are very difficult. However, this doesn't mean that there aren't amazing patterns, or choreographies, that allow multiple objects, planets say, to orbit one another. The solutions for two objects orbiting each other have been known for a very long time and essentially what we get are highly symmetrical orbits typified by the ellipses that planets follow in the solar system. As soon as you add an extra object, however, you can't find closed solutions. At first it was thought that the problem should be easy, but it resisted all attempts at a solution. Then, back in 2000, a highly symmetrical solution was found in the form of three planets following a figure of eight. After this lots of new complex orbits were discovered. We have looked at the simulation of some of these orbits before - The Magic Of N-Body Solutions. Now Gregory Minton has implemented an interactive JavaScript program, Choreo.2.3.js, that lets you try to find choreographies of your own. Here is one I found earlier:
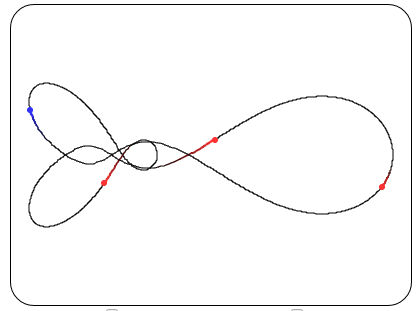
While you don't have to know anything about it to make use of it, the way that the program works is interesting. The principle is that it takes the path that you have drawn and finds its Fourier transform. This is very similar to the way that a Fourier series is used to draw general objects, in as explained in How To Draw Einstein's Face Parametrically. Then it numerically minimizes the action as a function of the Fourier components. This changes the shape of the curve until it generates a solution to the n-body problem. Sometimes the only solution close to the curve you have drawn is a circle or a figure of eight, which is rather disappointing, but with enough wiggles and crossings you can find interesting arrangements.
If you do find anything interesting then upload it and you might get to name it and have it added to the gallery. There are a number of other things to say about the orbits you find. Most of them aren't stable and in the real world they would decay at the slightest perturbation. So this means that you aren't actually going to find planetary systems with orbits as complex as these. This also makes numerical simulation of the orbits difficult as errors tend to accumulate. The animations shown on the web site are in fact exact animations based on the symmetry and the computed solution path. More InformationRelated ArticlesHow To Draw Einstein's Face Parametrically WebGL - Trojans, Snakes And Real Time Textures Babylon.js - A WebGL Game Engine From Microsoft
To be informed about new articles on I Programmer, install the I Programmer Toolbar, subscribe to the RSS feed, follow us on, Twitter, Facebook, Google+ or Linkedin, or sign up for our weekly newsletter.
Comments
or email your comment to: comments@i-programmer.info
|
| Last Updated ( Sunday, 11 January 2015 ) |