| Weather Control Via Chaos |
| Written by Mike James | |||
| Wednesday, 13 April 2022 | |||
|
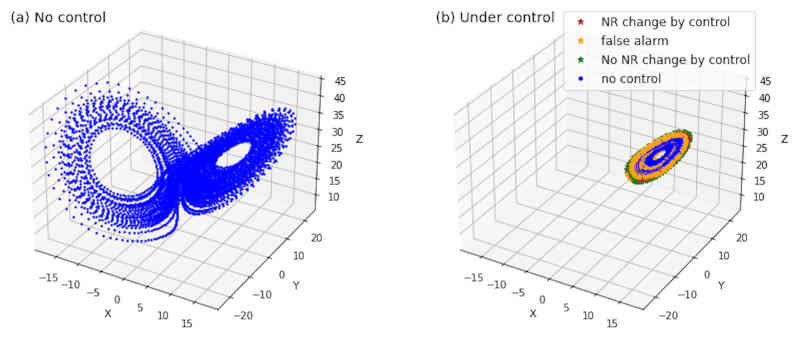
The weather is a chaotic system and the astonishing fact that the flap of a butterfly's wing can influence the development of a tornado is well known. Could this sensitivity be used to good effect? Could the flap of a butterfly's wing be used to change the weather in our favor? If it could it isn't only the weather that we could control as chaotic systems are everywhere. It all started back in 1963 when Edward Lorenz proposed a "simple" model of the atmosphere with three variables - x, the rate of convection; y, the horizontal temperature variation; and z, the vertical temperature variation. It isn't a very realistic equation, but the behavior of its solutions are expected to be broadly characteristic of the way the atmosphere behaves. The Lorenz 63 equations are also characteristic of a range of other physical phenomena - lasers, DC motors, chemical reactions and so on. The key point is that anything described by the equations exhibits chaotic behaviors. That is, tiny perturbations have big effects. In the case of the weather two almost identical initial conditions can develop into two very different outcomes a few days on. Thus the weather is in general sensitive to the flap of a butterfly's wings in that such a small change can, if you wait long enough, make a huge diference to the outcome. This butterfly effect has long been seen as a fundamental problem with trying to forecast any chaotic system, but it might be used to our advantage if instead of forecasting we turn our attention to controlling. Traditionally the problem with attempting to control the weather is that there is a lot of energy in the system. Trying to stop a hurricane would need the sort of energy released by a nuclear device - which is generally thought not to be a good idea. However if the weather system is chaotic then a small change could, after some time, produce a big effect and this is the idea taken up by a team of researchers led by Takemasa Miyoshi of the RIKEN Center for Computational Science in Kobe Japan. The idea has only been explored by simulation using the Lorenz 63 equations but they have been able to keep the system in within a chosen regime by applying small perturbations to the variables. To quote from the recent paper: We aim to apply “the control of chaos” to the weather. We do not aim to cause a permanent irreversible change to nature, but we would like to control the weather within its natural variability and to aid human activities, for example, by shifting the location of an extreme rain region to avoid disasters without causing a side-effect on the global climate. The experiment focused on keeping the system in one of two partly stable states - the wings of the butterfly. Normally the system settles into one of these two states and then chaotically flips to the other one. The purpose of the control is to keep the system in one of the wings. This would correspond to keeping a weather system in one state and supressing an undesirable change.
The control algorithm was remarkably simple. It relies on forcasting a set of outcomes given the system is run without intervention. If the system looks like it might be about to flip between the states a small perturbation is added to the model - corresponding to the action that would be taken to control the weather. Adding random perturbations didn't work. Taking the difference between models that changed state and ones that didn't change state as the perturbation did. You can see the effect of the control perturbation in the following video: You can see that the uncontrolled simulation flips between the two states, but the controlled version stays put. So is this weather control? No. The perturbations were added to variables that we would struggle to control. What is needed is a point perturbation, like the flap of a butterfly's wing, that can make a difference in the bulk of the process. What the experiment does is demonstrate is that trying to control chaos isn't a silly idea. The researchers plan to continue looking at the problem and I would suggest either finding a way to use a gradient approach or plug in a neural network to determine the perturbation.
More InformationControl simulation experiment with Lorenz's butterfly attractor Related ArticlesThe Programmer's Guide to Chaos The Chaos Within Sudoku - A Richter Scale Chaos Found In Weather Forecast -Same Code, Different Computer, Different Results To be informed about new articles on I Programmer, sign up for our weekly newsletter, subscribe to the RSS feed and follow us on Twitter, Facebook or Linkedin.
Comments
or email your comment to: comments@i-programmer.info
|
|||
| Last Updated ( Wednesday, 13 April 2022 ) |