| Stanford Engineers Build A Water Droplet Based Computer |
| Written by Harry Fairhead | |||
| Wednesday, 24 June 2015 | |||
|
It is well known to every computer scientist that you can implement a computer in many different ways - but drops of water? Yes of course you can and the result is really fun to watch. Ok so you can build computers out of any physical system that has the ability to implement logic gates - in fact just one gate will do. All you need in principle is a Nand or a Nor gate and you can use it to create all the rest. To an extend once you know this fact computers built from strange things - A Crab-Based Computer - becomes slightly less surprising, but no less entertaining. Researchers at Stanford, Georgios Katsikis, James S. Cybulski and Manu Prakash have created something new - a synchronous water droplet based machine. In this particular case you only have to watch the video of the computer in action to appreciate it at an aesthetic level:
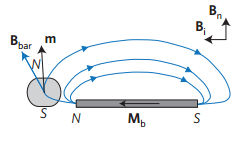
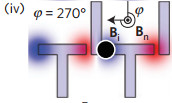
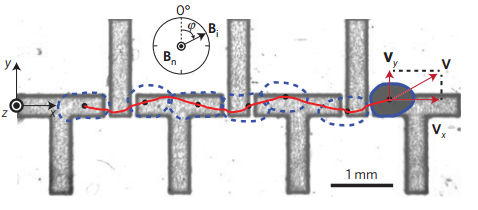
When you see the blobs of water moves around the grid it looks like some sort of complex dance or a complex game of pacman. The reason that everything looks as if it is in step is that it is. This is one of the few examples of a synchronous computing device built in an unlikely medium. We could leave it at this point - marveling in the way it all looks - but if you are anything like curious you will want a small clue as to how it works. First the transport mechanism. The the cause of the blobs moving is ingenious. First there is a constant vertical magnetic field which polarizes the ferro liquid so that it is like a small vertical bar magnet with the south pole closes to the substrate. The distance of the north pole from the substrate means that you can most ignore its interaction and consider the droplet as if is was just a single south pole - i.e. an approximate monopole. You can see a more accurate picture of how it interacts with a magnetized bar on the substrate in the picture below:
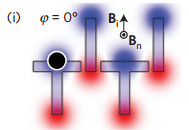
This is the first clever part. The second is that a rotating magnetic field is used to change the induced magnetization of the shapes in the substrate so as to create a "walking" magnetic wave that moves the blobs on. The magnetic field is switched through four positions at right angles and you can see how this moves the blob in the following four diagrams: In the first the rotating field points "up" and the everything is polarized so that it has a north pole (red) at its bottom end. In this case the blob is attracted to the simple vertical bar to its right - the nearest north pole.
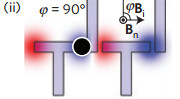
The field is then rotated through 90 degrees so that it is pointing to the right. Now everything is polarized so that the north pole is to the left. Notice the simple vertical bars don't really have an effect in this case and the blob moves to the north pole of the T bar to its right - again the nearest north pole.
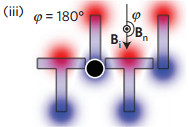
Now the field swings round to point down in the diagram and you have a repeat of the first step but with north and south swapped over. Everything is polarized in the vertical direction but with north poles at the top. This attracts the blob to the middle of the T bar to its right.
The final step should now be obvious. The magnetic field moves so that it points to the left and we have the setup in step two, everything is polarized in a horizontal direction but with north poles at the right. Now the blob moves to the right side of the T bar and the cycle is ready to repeat.
Clever! As the whole thing is symmetric it will work with the track in indirection.
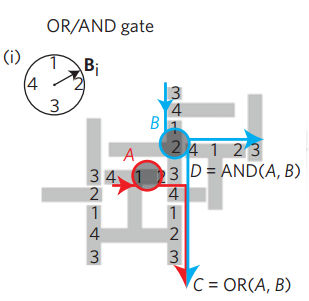
Ok so that gives you transport what about logic? To explain how gates work lets look at a simple And/Or circuit:
Notice that physical logic often does compute both And and Or at the same time because they are reversible and no information is lost. The key to understanding what is going on is to remember the blobs are south poles and so repel each other. If there is only a blob at A in the gate then the bars are arranged to take the it down the red path - and yes that is an example of a corner. The numbers show the position of the north pole at each clock cycle and you can see it is dragged around the corner. If there is a single blob at B then it moves straight down the blue line to C. If you look at the way the numbers are on the track you can see that this is so. So if there is a single blob at one of A or B we get an output at C and none at D. Now suppose that there is a blob at A and one at B. At the next clock cycle the blob at A moves forward and gets to 3 first because it is at the end of a T bar and so closer. The blob at B is repelled by it and has to move to the right and so follows the horizontal blue path. So if there is a blob at A and B we get an output at C and one at D. A little thought should convince you that C gives you A OR B and D gives A AND D. Other logic gates are similar. The paper has a much more precise analysis of what happens - any errors in this more direct explanation ore mine. It also explains additional devices like flip-flops and memory. They also give a set of design rules that enable you to take logic gates and other functional blocks and simply put them together as if you were designing a standard IC based circuit. If you want to give it a try there are design tools - the Lego Digital Designer and EAGLE CAD that you can use to create your own demonstration circuits. There is a walk though to get you started and an invitation to upload your designs to a gallery. Of course this isn't about building a really really slow computer using water drops. This is really about making material movement as logical as a computer. The sorts of things that the authors have in mind are chemical processing, analysis and so on - mesoscale material processing. Only time will tell what sorts of applications there might be for this approach but in the mean time we can just have fun watching it and designing new circuits. More Information
Related ArticlesSlime Mold Simulates Canadian Transport System A Water Droplet-Based Computer
To be informed about new articles on I Programmer, install the I Programmer Toolbar, subscribe to the RSS feed, follow us on, Twitter, Facebook, Google+ or Linkedin, or sign up for our weekly newsletter.
Comments
or email your comment to: comments@i-programmer.info
|
|||
| Last Updated ( Wednesday, 24 June 2015 ) |