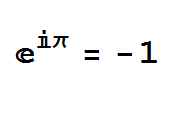| Google Doodle For Euler & His Beautiful Equation |
| Written by Historian | |||
| Monday, 15 April 2013 | |||
|
Today is the 306th anniversary of the birth of Swiss mathematician and physicist, Leonhard Euler and to celebrate we have a Google Doodle that brings together some of his most important mathematical discoveries Leonhard Euler is generally considered the greatest mathematician of the eighteenth century and one of the greatest mathematicians to have ever lived. His output was prodigious; his work fills about 80 volumes and much of it dates from the last two decades of his life, when he was totally blind.
Leonhard Euler April 15, 1707 - September 18, 1783
Born in Basel, Switzerland he spent most of his adult life in St. Petersburg, Russia, and in Berlin, Prussia. He made important discoveries in fields as diverse as infinitesimal calculus and graph theory. He also introduced much of the modern mathematical terminology and notation, particularly for mathematical analysis, such as the notion of a mathematical function.
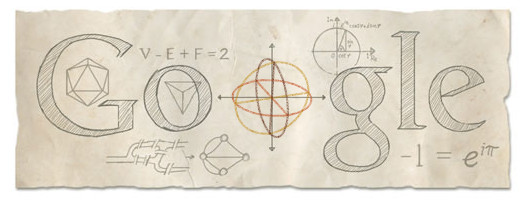
The Google Doodle recalls several of his legacies. Perhaps the most significant is the Euler Equation which reveal a relationship between e, pi and i and has been described as "the most beautifual equation in all mathematics. The geometrical form of the equation is also in the Doodle:
You will notice polyherda inside the G and initial o. This is a reference to Euler's polyhedron theorem:
V - E + F = 2
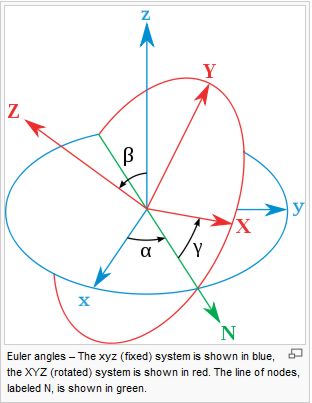
which characterizes the surface of any convex polyhedron in terms of its vertexes, edges and faces. In the center of the Doodle we encounter an animation of Euler angle, which describe the orientation of a rigid body in 3-dimensional Euclidean space.
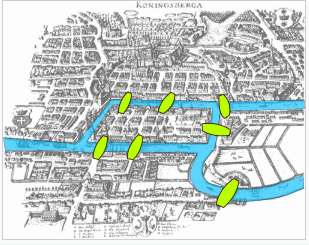
The bottom left of the Doodle refers to the problem known as the Seven Bridges of Königsberg, which Euler solved in 1736. The city of Königsberg, Prussia was set on the Pregel River, and included two large islands which were connected to each other and the mainland by seven bridges.
The problem is to decide whether it is possible to follow a path that crosses each bridge exactly once and returns to the starting point. Euler was able to prove this was impossible and his solution is considered to be the first theorem of what we now call graph theory and which is fundamental to the study of networks both social and physical. What would have Euler achieved had he been born into the computer age? Or would he have scoffed at the idea of needing a calculating engine. He was able to do prodigious calculations in his head, a necessity after he went blind. The contemporary French mathematician Condorcet told the story of two of Euler's students who had independently summed seventeen terms of a complicated infinite series, only to disagree in the fiftieth decimal place; Euler settled the dispute by recomputing the sum in his head.
More InformationEuler characteristic (Wikipedia)
To be informed about new articles on I Programmer, install the I Programmer Toolbar, subscribe to the RSS feed, follow us on, Twitter, Facebook, Google+ or Linkedin, or sign up for our weekly newsletter.
Comments
or email your comment to: comments@i-programmer.info
|
|||
| Last Updated ( Monday, 15 April 2013 ) |