| SparkleVision - Seeing Through The Glitter |
| Written by Mike James | |||
| Wednesday, 14 January 2015 | |||
|
Another new application of computational photography lets you reconstruct an image that has been reflected by a rough shiny object - a glitter-covered surface, say.
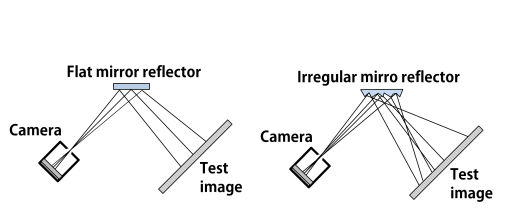
This is a classical application of signal processing theory. A signal has been transformed so that it isn't usable. To restore the signal back to its original state all you need is the inverse transformation. Of course, the devil is always in the detail and making such simple schemes work is usually much more difficult than anyone ever expects. In this case the transformation isn't one that you might think of as a transform. If you have an image viewed by reflection from a "glittery" surface - more technically one containing mirror facets with random orientation - then what you will see is a blurry shadow of the original. This isn't unreasonable as the rays that should have reached your eye or the camera have been randomly reflected by the surface. The image has been scrambled.
To unscramble the image all you need is the inverse transform and a recent paper by Zhengdong Zhang, Phillip Isola, and Edward H. Adelson of MIT explains how to get one. To summarize it main points If an image is reflected off a flat mirror the rays arrive where they should to form the image. If however the image is reflected off a "smashed mirror" they arrive at different locations. The key observation is that you can regard the effect as a linear transformation of the image. To create the inverse transformation what you have to do is probe the system by displaying test images and seeing what the result is. From this data you can work out how the surface scrambles the rays and derive an inverse. For example, if the test image is a single point of light then it will bounce off a small number of random mirrors and create an image with a small number of bright spots. This gives you the forward transform for that pixel and from this you can derive the inverse. Repeat this for all of the pixels in the image and you have a complete inverse. The actual method makes use of many test images that include each pixel more than once to minimize random noise. The inverse transform is found by a constrained least squares. So does it work? Given good conditions it seems to work.
There is one big problem with the method and this is that it is sensitive to misalignment. Even shifting the test image by one pixel makes the reconstruction much worse. This might seem to make reconstruction impossible in some situations, but as the researchers point out you could search for the best image by reconstructing it with different shifts. It might even be a useful way of detecting small movements. It is also suggested that the reflections could be used as a lightfield camera to capture some 3D information - how exactly is future work. Are there any practical applications of the technique as it stands? Clearly it could be used in surveillance. Who would think that a glitter ball or mirror could reveal the details of what is going on in a room. The calibration needed to reconstruct the image could be done before or after snooping was over.
More InformationSparkle Vision: Seeing the World through Random Specular Microfacets Related ArticlesSee Invisible Motion, Hear Silent Sounds Cool? Creepy? Computational Camouflage Hides Things In Plain Sight Google Has Software To Make Cameras Worse Plenoptic Sensors For Computational Photography
To be informed about new articles on I Programmer, install the I Programmer Toolbar, subscribe to the RSS feed, follow us on, Twitter, Facebook, Google+ or Linkedin, or sign up for our weekly newsletter.
Comments
or email your comment to: comments@i-programmer.info
|
|||
| Last Updated ( Wednesday, 14 January 2015 ) |