| Seeing Around Corners |
| Written by David Conrad | |||
| Sunday, 12 November 2017 | |||
|
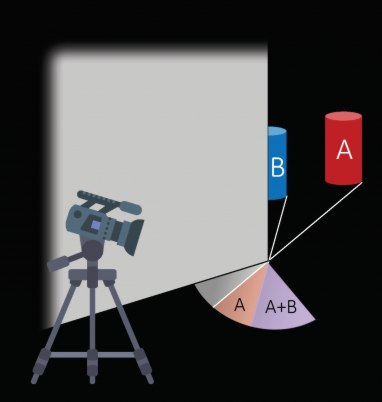
A team from CSAIL has come up with an innovative algorithm for eliminating blind spots. The idea is that you use corners as a camera. Sound mad, but it is just another example of an inverse problem that can be solved. Inverse problems are both fun and very important. You start out with a model of how some data can be produced, usually with a lot of parameters that vary the pattern of data. Then you collect some data and use it to work back to the set of parameters that generated the data. It sounds really dull and boring, but this is the principle of the CT scanner. Take an X-ray source and pass it through a solid object. Measure the intensity of the X-rays that pass though at various angles and then solve the inverse problem to work out what is inside the object. This sounds more exciting and, yes, in general inverse imaging problems are more interesting and impressive than more abstract problems. Seeing round corners is the inverse problem solved in Turning Corners into Cameras: Principles and Methods by CSAIL researchers Katherine L. Bouman, Vickie Ye, Adam B. Yedidia, Fredo Durand, Gregory W. Wornell, Antonio Torralba and William T. Freeman. The idea is simple enough to explain. The light intensity of the floor around a corner is a mixture of the light that reaches it from different angles around the corner. You can see this idea in the diagram taken from the paper:
Another way to understand this idea is to imagine what you see as you walk up away from the corner. You slowly see more and more "around the corner" and this corresponds to the variation in the angle of light that reaches the floor. You can work out a mathematical model of what the light on the floor would be given the illumination around the corner as a function of the angle. Now you measure the light and solve the inverse problem. The result is a 1D map of the scene that is hidden by the corner. You can see this in action in the video: Having a 1D view of the scene around the corner isn't exactly like getting a full image, but in some situations it may be enough to tell you what you need to know - like how many people are there and how are they moving. With two corners, e.g. a doorway, you can capture 1D images that are offset so that you can work out a 2D position from the "parallax" effect. It is interesting to note that the color variations on the floor aren't intense enough to be seen by the human eye, but you only need a standard video camera, a phone camera even, to get data that is good enough to solve the inverse problem with reasonable accuracy.
As the conclusion to the paper states: "Since nearly every corner now offers a 1-D view around the corner, this opens potential applications for automotive pedestrian safety, search and rescue, and public safety. This ever-present, but previously unnoticed, 0.1% signal may invite other novel camera measurement methods." So keep in mind the inverse problem as you think about what you see. There may be more information encoded into it than you initially imagine and it may be recoverable.
More InformationAn algorithm for your blind spot Related ArticlesSeparating Reflection And Image Time-Lapse Videos From Internet Photos Automatic High Dynamic Range (HDR) Photography The Display That Does Away With Glasses Plenoptic Sensors For Computational Photography
To be informed about new articles on I Programmer, sign up for our weekly newsletter, subscribe to the RSS feed and follow us on Twitter, Facebook or Linkedin.
Comments
or email your comment to: comments@i-programmer.info |
|||
| Last Updated ( Sunday, 12 November 2017 ) |