| The Magic Of N-Body Solutions |
| Written by Mike James | |||
| Saturday, 24 August 2013 | |||
|
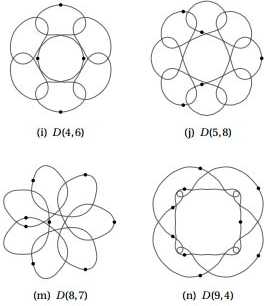
The physics of n-body problems isn't something everyone can appreciate as mathematics, but as an animation there is no barrier to understanding and being amazed. The n-body problem sounds dry and dusty. The problem is to work out the paths that n-bodies follow under their mutual gravitational attraction. The problem of n=2, i.e. the two body problem, was worked out a long time ago and it's the approximation we use to work out the theoretical orbits of the planets. For just two bodies we can work out exact solutions for the general case. The behaviour is fairly simple the two bodies rotate around their combined center of mass and this gives rise to the familiar stable elliptical orbits we see in, say, the solar system. While working with two bodies is easy, extending the problem to even 3 bodies proves to be surprisingly difficult. So much so that we don't have exact solutions in the general case and we tend to have to rely on simulation or on perturbation theory. However, just because you can't find a general solution it doesn't mean that you can't find solutions in special cases. In 2000 a set of stable orbits for n bodies was discovered and since then people have been working towards a complete classification of these very special cases.
Yes these are possible gravitational orbits!
Seeing n-bodies move in a stable orbit around each other looks a lot like a dance in progress and hence they are called choreographies. Now a new paper by Montaldi and Steckles gives a complete classification of the symmetries that such choreographies can have. Dan Gries has used this to create an interactive animation of some of the major types and it is fascinating to watch.
You really do need to see the animations in progress to appreciate the amazing symmetry in time and space. What you have to keep in mind as you watch the animations is that these objects are moving under their own gravitation and they have to "balance" their mutual distances to produce a force in the direction that you see them move in. This is easier to understand in the simpler two-body systems. If this doesn't impress you, then consider the fact that you could get a set of stars or other bodies actually following these orbits. Do they exist anywhere? The program is written in JavaScript using three Canvas objects stacked on top of one another to create the trails that slowly fade to almost black, read Dan Gries' account for the fine detail. The program doesn't work by simulating the gravitational mechanics but uses the periodic description of the obits in the form of a Fourier series. This is very similar to the way that a Fourier series is used to draw general objects in as explained in How To Draw Einstein's Face Parametrically.
More Informationn-body choreographies animation N-body planar choreographies: illustrating mathematics in HTML5 canvas Classification of symmetry groups for planar n-body choreographies
Related ArticlesWebGL - Trojans, Snakes And Real Time Textures Babylon.js - A WebGL Game Engine From Microsoft
To be informed about new articles on I Programmer, install the I Programmer Toolbar, subscribe to the RSS feed, follow us on, Twitter, Facebook, Google+ or Linkedin, or sign up for our weekly newsletter.
Comments
or email your comment to: comments@i-programmer.info
|
|||
| Last Updated ( Saturday, 24 August 2013 ) |