| Optimize Mining Bitcoin |
| Written by Mike James | |||
| Wednesday, 27 November 2013 | |||
|
The focus of mining Bitcoin ever faster is to use custom hardware, but what about the algorithms? How much effort has been expended on optimizing the proof of work task? It is a tough problem, but it could save a lot of energy and make some money.
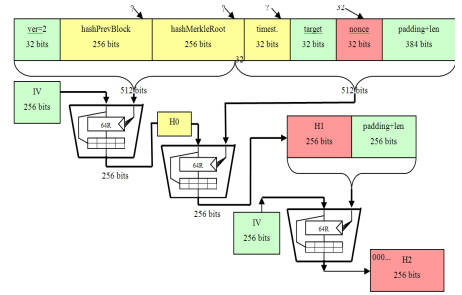
At the moment to create new Bitcoins a miner has to solve a cryptographic problem. When they have solved the problem they have verified a block of Bitcoin transactions and they get some newly-minted Bitcoins for their trouble. The big problem with this is that the algorithm contains a difficulty factor which is adjusted to make the time to solve the problem roughly constant at about 10 minutes. This is only a problem because as time goes on Bitcoin miners are throwing ever more hardware at the problem in an effort to be the first to solve the block. At first, spare CPU cycles were enough, then GPUs were needed, and now you have to use a custom mining machine. Even though custom mining machines do their best to reduce their power consumption the total power being used to mine Bitcoin is surprising - just short of 1000 Megawatt hours per day. Finding a way to improve the algorithm will save a lot of power and this is the problem that three security researchers, two from University College London, set out to tackle in new paper The Unreasonable Fundamental Incertitudes Behind Bitcoin Mining. As well as considering algorithmic efficiency, the paper also considers many other issues, but it is its central section that is most interesting to developers. The mining problem is to find a 32-bit value that when added to the current block gives an SHA-256 hash that is smaller than a specified value. As the SHA-256 hash function is complex, and there is no easy-to-compute inverse function, mining involves computing the hash for trial values from 0 to 2^32, i.e. an exhaustive search. Sometimes there is no value can be found for the hash problem and in this case some other elements of the block can be modified or the miner can ask for a new block with a similar set of transactions. So the huge electricity bill comes from the need to compute the SHA-256 hash function a lot of times. Clearly to make the mining go faster all we have to do is speed up SHA-256. For arbitrary data this would be a very difficult task, but for a Bitcoin block it is easier because we are computing the hash of mostly the same data over and over. However, the details are complicated. The SHA-256 hash is actually used twice in the Bitcoin algorithm. First the 640 byte block is padded to make it 1024 bytes. Then the SHA-256 ia applied to produce a 256-bit hash which is then padded to 512bytes and hashed a second time. The first trick is that the SHA-256 hash is based on the use of a block cypher that works in 256-byte blocks using a 512-byte key. To make it work as a hash, the data input is fixed and the data from the block is used as a 512-byte key, producing a 256-byte hash. If you want to hash more than 512 bytes then the cypher is used as many times as needed. So in the first hash computation it is used twice and in the final hash it is used once. If you are prepared to break open the black box that is the SHA-256 hash then you can regard it, in the Bitcoin case, as being three applications of the cypher - as shown in the diagram below (taken from the paper):
The red blocks indicate data that change each time the trial value is modified. You can see that once the hash on the first 512 bytes has been computed you don't have to do it again. This is a big saving. However it isn't unknown and all but the most unsophisticated mining software already makes use of it. From here the paper explores other improvements in the algorithm, mostly delivering only small speedups compared to the obvious big one. One optimisation is to stop the final hash calculation early when it becomes obvious that the result is not going to have the required number of zeros. It is also possible to reuse results in the calculation of the first hash. Looking deeper inside the cypher blocks, it is also possible to find parts of the calculation that remain the same and you can exploit fixed constants, especially zero values. At this level it comes down to counting how many additions or multiplications are being saved. Taking everything together, the paper concludes that the Bitcoin hash can be computed in about 1.86 applications of the cypher function, whereas a naive approach needs 3. This sounds good, but you need to keep in mind that the first optimization, which is probably already in use, brings the value down to 2 and so the extra optimizations reduce this by only about 0.14 The real value of this work is to open up the possibility that, due to regularities in the computation, there might be even better ways of computing the SHA-256 hash in the case of Bitcoin. Just because the hash is difficult to invert in the general case this might not hold in the specific case of Bitcoin. It is also worth exploring the possibility that computing trial values in a particular order might lead to a faster iterative approach using results from each computation more efficiently in the next. Whatever the success of such efforts, it is worth keeping in mind that such an improvement would be temporary. The Bitcoin algorithm sets the difficulty level of the problem to keep the time to solve at around ten minutes. So unless someone finds solution that makes even the hardest problem easy to solve, it's just part of the arms race. Of course, if this was to happen the Bitcoin algorithm would be broken.
More InformationThe Unreasonable Fundamental Incertitudes Behind Bitcoin Mining
Related ArticlesIs Bitcoin Broken - A Response And A Conference Hardware Mines Bitcoins Faster Bitcoin Hits 10.5 Million - Mining Payment Halves Bitcoin Idea Gets $500,000 funding Bitcoin still standing - but panic takes over Inside Bitcoin - virtual currency Bitcoin gains an open source client Digital currency lets GPU cycles print money Hashing - The Greatest Idea In Programming
To be informed about new articles on I Programmer, install the I Programmer Toolbar, subscribe to the RSS feed, follow us on, Twitter, Facebook, Google+ or Linkedin, or sign up for our weekly newsletter.
Comments
or email your comment to: comments@i-programmer.info
|
|||
| Last Updated ( Wednesday, 27 November 2013 ) |