| A New Computational Universe - Fredkin's SALT CA |
| Written by Mike James |
| Tuesday, 03 July 2012 |
|
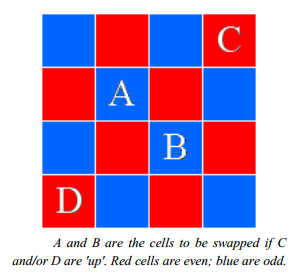
Edward Fredkin believes that a final grand theory of everything would be computational - that the universe is a computer. Now we have an example of an extremely simple computational system - a Cellular Automata - that has particles that attract and repel, orbit and decay with a half-life law. Cellular Automata (CA) are prime candidates for the sort of final theory of everything that we are looking for. They obey simple rules and yet they produce complex behaviors. One of the best known CAs is John Conway's Life and after a long time studying it we are still making discoveries. Until recently there ware no CAs that exhibited the sorts of behavior that physicists might find interesting. For example, CAs do not in general exhibit motion in a circle, or wave motion. In a recent paper Edward Fredkin and Daniel Miller have explained that their latest discovery - a 3D CA does exhibit circular motion and many other types of behavior characteristic of classical physics. This may not mean that they have found the fundamental theory, but it is interesting. The new CA is a modification of Fredkin's earlier SALT architecture in which every cell is identified as either even or odd - as in sodium and chlorine in a salt crystal hence the name. The state of each cell is either up or down and the development rule simple takes account of states of odd and even neighbours. The up-date at each time step simply takes the form of a swap of the states of diagonally related cells. SALT CAs are reversible and capable of universal computation and are conjectured to be capable of universal construction in the sense of Von Neumann. After looking at a range of possible rules for SALT CAs, one particular type has been selected and explored in detail - Busy Boxes. The 2D version of the CA is easier to explain. The rule is to swap the diagonal cells A and B if the cells in the "Knight's move" positions, i.e. C and D have particular states. Notice that C and D are always of opposite parity to the cells being swapped:
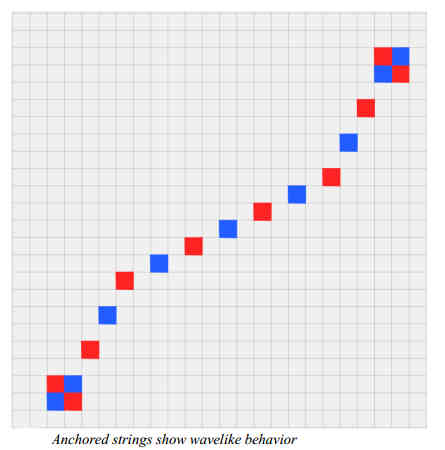
The 2D rule can be extended to 3D by using it on each of the 3D planes defined by the axes. Even in its 2D form, the CA exhibits "strings" which move along as units that are never created or destroyed and which show string-like oscillation.
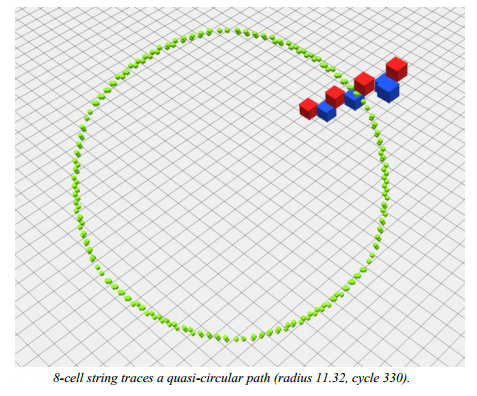
Once you move to 3D, small particle-like blocks move as a unit in any of 8 directions - like gliders in Life - but they also move in circular orbits.
You can see a video of the string rotating in the following video, but playing with the real thing is much more impressive:
They also engage in decay processes which follow an exponential law, like real particles do. It is easy to think that this is trivial behavior, but a digital rule producing exponential behavior is interesting. All of the simulations are available on a website and you can setup your own starting configurations. The paper concludes: The Busy Boxes variant of the SALT family of reversible cellular automata has shown itself to possess an intriguing number of features that are worthy of further study and analysis. Physicist Gerard T'Hooft has written about the possibility that reversible CA's such as this one may help elucidate some aspects of physics in the quantum realm [5]. We believe that the study of emergent, qualitative, and statistically predictable behavior of these kinds of discrete, deterministic systems can indeed shed light on questions in physics, and may also help to clarify the deeper principles of entropy and the origin of complex, selfpropagating systems such as those found in our biosphere There are some theoretical imperfections in the nature of rule and there are lots of questions that need to be answered. It looks like a good area to get involved in for amateurs and professionals alike.
More InformationCircular Motion of Strings in Cellular Automata, and Other Surprises (pdf) The Busy Boxes Simulation: The orbiting string simulation:
Related ArticlesA Computable Universe - Roger Penrose On Nature As Computation
Comments
or email your comment to: comments@i-programmer.info
To be informed about new articles on I Programmer, install the I Programmer Toolbar, subscribe to the RSS feed, follow us on, Twitter, Facebook, Google+ or Linkedin, or sign up for our weekly newsletter.
|
| Last Updated ( Tuesday, 03 July 2012 ) |