| Goldbach Conjecture - Closer to Solved? |
| Written by Mike James |
| Sunday, 13 May 2012 |
|
The Goldbach conjecture is not the sort of thing that relates to practical applications, but they used to say the same thing about electricity. The Goldbach conjecture is reasonably well known: every even integer (>2) can be expressed as the sum of two primes. Very easy to state, but it seems very difficult to prove. If you try it out via a small program you wil very soon convince yourself that it works for any integer you care to use as a test case. However, this is not a mathematical proof and there may just be an integer out there waiting to be found that needs three or more primes in the sum.
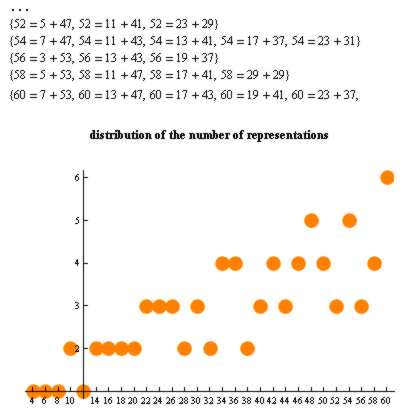
The number of prime sum representations of small integers (Source Wikipedia) There are a number of variations on the basic Goldbach conjecture that are often studied as a sort of warm up to the real thing. For example, the Odd Variant postulates that every odd number greater than 7 is the sum of three odd primes. This was proved, but the proof relied on a modification of the Riemann hypothesis - which is as yet another unproven, well-known, challenge. To date there have been a smattering of proofs that set bounds on the size of a number that disobeys the conjecture - every sufficiently large odd integer is the sum of three primes and almost all even integers are the sum of two primes. You might think that "sufficiently large" would mean that we could take a program and test the numbers up to the upper bound where the proof takes over. Unfortunately the upper bounds are very "upper" , for example bigger than 106846168, which makes computational help still out of reach. Now we have another proof that places a different sort of upper bound on the conjecture. Terence Tao, a Fields medalist, has published a paper that proves that every odd number greater than 1 is the sum of at most five primes. This may not sound like much of an advance, but notice that there is no stipulation for the integer to be greater than some bound. This is a complete proof of a slightly lesser conjecture, and might point the way to getting the number of primes needed down from at most five to at most 2. Notice that no computers where involved in the proof - this is classical mathematical proof involving logical deductions rather than exhaustive search. So does this have any application to real world problems? I doubt it, but number theory is so central to coding and cryptography that I'm probably wrong. On another note it is a demonstration that mathematics hasn't fallen to computer-based constructive proofs just yet and perhaps there is still a neat one-page proof of the four-color theorem waiting to be written. via: Math Drudge More InformationRelated ArticlesTravelling Salesman - A Movie About P=NP
Comments
or email your comment to: comments@i-programmer.info
To be informed about new articles on I Programmer, subscribe to the RSS feed, follow us on Google+, Twitter, Linkedin or Facebook or sign up for our weekly newsletter. <ASIN:1582341281> <ASIN:9812381597> <ASIN:0471462349> |
| Last Updated ( Monday, 14 May 2012 ) |