| The Computer Science Breakthrough Of The Decade Now Reinstated! |
| Written by Mike James |
| Tuesday, 10 January 2017 |
|
This is almost unprecedented. First we have a major result in computer science. A couple of months later it is suddenly retracted, causing a wave of disappointment through the community. But to our great relief it is reinstated after only a few days. Is math getting sloppier? Are proofs receiving far too little attention before they are announced? No, it is just that the average proof is getting more complex. We are probably entering an era where proofs have to settle and mature like fine wine before we can believe them. And yes it is strange to use the term "believe" when it comes to a purely logical subject like math but modern math proofs are built on so many other results that it is a matter of verifying a house of cards from the top down. There is also the long standing matter of have you covered all the possibilities. It is something unwritten, but it is well known, that any mathematical proof has to deal with all the ways that something can or cannot happen and what if you have just missed a whole new way of doing something? After claiming the breakthrough in 2016 László Babai, posted a retraction on January 4th, 2017. Now we have a post that claims the proof has been repaired: January 9, 2017 update: quasipolynomial claim restoredOn January 4 I announced that Harald Helfgott pointed out an error in the analysis of my Graph Isomorphism test. The error invalidated my previous claim of quasipolynomial efficiency. The text of the announcement is appended below. On January 7 I discovered a replacement for the recursive call in the "Split-or-Johnson" routine that had caused the problem. With this modification, I claim that the Graph Isomorphism test runs in quasipolynomial time (now really). The replacement consists of a few lines of pseudocode, analyzed via a simple new lemma on the structure of coherent configurations. I am working on an updated arXiv posting. Remarkable - who would have thought that math had such drama in it? Well anyone with any contact with mathematics of course!
The update and original news item follow below:
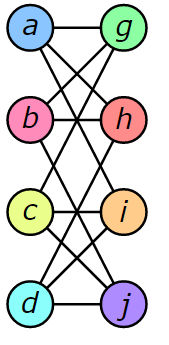
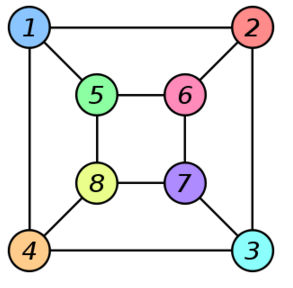
Graph Isomorphism Update January 4, 2017 It might sound overly dramatic, and when you discover what it is you might want to use the term "esoteric", but the discovery of a quasipolynomial time algorithm for the graph isomorphism problem is interesting and important and was big news back in 2016. Now we have a snag. Its originator, László Babai, posted a retraction on January 4th, 2017. This isn't a good start to 2017 but credit to László Babai for being so open about it. The result was important, see the original news report appended below, and so it has been examined carefully. Unfortunately, while there is nothing wrong with the bulk of the paper, there is a flaw in the timing analysis that alters the result from quasipolynomial time to subexponential time. "The technical content of the paper remains virtually unchanged. The previous analysis breaks down for one of the recursive steps of the combinatorial "Split-or-Johnson" procedure; but the "Split-or-Johnson" theorem remains valid with the updated timing analysis. All other results are unaffected. I am working on an updated arXiv posting (with a different title) that will also improve the presentation, following comments from several colleagues. I wish to thank Harald Helfgott (University of Göttingen and CNRS) for spotting this error and for spending months studying the paper in full detail. Helfgott will publish his exposition of the algorithm (with the revised analysis) in the Bourbaki Seminar series." The result is still impressive, but not the breakthrough of the decade -which was probably an over-the-top journalistic headline anyway. There is also scope for hope that the proof can be fixed up: "Thanks to Harald's efforts and his unfailing attention to the most seemingly minute detail, I am now confident that the result, with the revised analysis, stands. Moreover, the new techniques introduced in the paper provide a framework and tools for further progress." It is also a great example of modern mathematics being so complex that a proof is not a proof until it has stood for a long time. We like to think that a proof is a sequence of verifiable deductions leading from premise to theorem, but clearly today what "verifiable" means is something different from what it meant in the days of Euclid. Perhaps we do need computer help with our proofs. What follows is the news Item I wrote back in October 2016 and it needs to read with the appreciation of the excitement of a new discovery: László Babai has posted a abstract of a talk he is presenting on Tuesday, November 10, 2015 in Chicago: We outline an algorithm that solves the Graph Isomorphism (GI) problem and the related problems of String Isomorphism (SI) and Coset Intersection (CI) in quasipolynomial (exp(polylog n) time. If he has indeed come up with such an algorithm it will charge the whole landscape of Computer Science so some background to explain this claim is required. First we have to find out what the graph isomorphism problem is and it isn't as difficult at sounds. A graph is a collection of nodes and arcs that connect the nodes - think of a road network. The graph isomorphism problem is simply to decide if two graphs are identical. This sounds easy but you have to find with node corresponds to which node. For example these two graphs look different but they are in fact the same::
Credit: Wikipedia The colors give you the mapping between the two that reveals that they are identical or isomorphic - same shape. This is a decision problem - are the two graphs isomorphic - and it looks difficult. How hard a problem is can be measured by the way in which the time required to solve the problem increases as the size of the problem goes up. For example, if the time for the graph isomorphism problem goes up nc where n is the number of nodes in the graph and c is some constant, then it is polynomial difficulty. It seems, at first sight that graph isomorphism is a much more difficult problem and probably takes time exponential in the number of nodes - i.e. something like cn Notice that cn gets bigger than any polynomial you care to consider, e.g. c2 c3 c4 and so on as n gets bigger and bigger. OK, so finding a solution to the graph isomorphism problem is tough, but if I give you a solution, i.e. a list of node mappings that I claim is an isomorphism, you can check my solution very quickly. Problems with the property that proposed solutions can be checked very quickly, i.e. the checking algorithm runs in polynomial time, are in a class of problems called NP Nondeterministic Polynomial time. All easy problems, i.e. those that can be solved in Polynomial time and hence are in P, are also in NP because you can obviously check a solution in polynomial time as well. The two complexity classes, P and NP, are at the core of computer science. One question that we really want to answer is are P and NP different or the same. It seems that some problems in NP seem much more difficult - these are the NP complete problems. It can be shown that if an NP complete problem has a polynomial solution then so does every NP complete problem and hence P=NP. If P=NP then bad things are probably going to happen because a lot of encryption relies on NP complete problems being difficult to solve and if they are in P they are not difficult enough. Now we return to the graph isomorphism problem. This is one of the few well known problems in NP that hasn't been proved to be in P or in NP complete and after the latest result we still don't really know for certain, but it doesn't really matter.
The next question we need to answer is what is quasipolynomial time. Another way to write a polynomial time is: nc = ec(loge n) which you can see is true because loge n is what you have to raise e by to get n. Quasipolynomial time is: ec(loge n)^k for some k which reduces to polynomial time for k=1. So the result we have, assuming Babai's proof is validated, is that a problem that is in NP that hasn't been proven to be NP complete has a quasipolynomial time algorithm. The point being that this is so close to polynomial time that it makes little difference. So what does this mean for NP=P? It means an example of an NP problem that at first look appears exponentially hard isn't. There have been other examples of this in the past - proving a number was prime or not was thought to be in EXP but recently an algorithm was found that was in P. Could it be that other NP problems that appear to be in EXP are quasipolynomial? Could it be that an NP complete problem like factoring could be quasipolynomial? You might argue that if NP complete problems were quasipolynomial then NP still isn't P, but as far as practicalities such as encryption are concerned they would be practically equal. You could say that you don't need to prove NP=P proving NP=QP is enough. What is surprising is the amazing theoretical tools that seem to be essential to proving this sort of result. The suggestion is that the proof relies on the classification of the simple groups. Are such advanced methods really needed to find efficient algorithms? Probably. More InformationGraph Isomorphism update January 4, 2017 A Big Result On Graph Isomorphism Related ArticlesTravelling Salesman - A Movie About P=NP
To be informed about new articles on I Programmer, sign up for our weekly newsletter, subscribe to the RSS feed and follow us on, Twitter, Facebook, Google+ or Linkedin.
Comments
or email your comment to: comments@i-programmer.info |
| Last Updated ( Tuesday, 10 January 2017 ) |