| Complexity Theorist Awarded 2014 Abel Prize |
| Written by Mike James | |||
| Wednesday, 02 April 2014 | |||
|
The Abel prize is sometimes called the Nobel Prize for mathematics, but then so is the Fields medal. The good news this year is that the recipient, Yakov G Sinai, is known for his work in computational complexity.
The Norwegian Academy of Science and Letters established the Abel Prize, which is worth 6 million Norwegian kroner (around $1 million US) in 2003. This year it has been awarded to Yakov G Sinai "for his fundamental contributions to dynamical systems, ergodic theory, and mathematical physics".
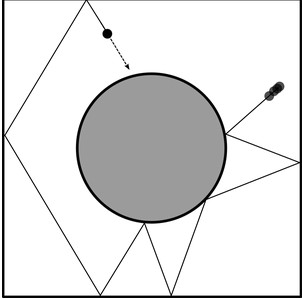
Sinai's first contribution was to the study of ergodic systems. You might be forgiven for asking "what systems"? We often make the assumption that observing something across a single system is the same as making an observation across many systems of the same type. For example, if you have a physical random number generator then you generally assume that switching it on and making a measurement of the mean of the data it produces would give you the same answer if you switched it on and off many times and measured the mean of each series it produced. You assume that the random number generator is "ergodic" because you believe that switching it on and off has no effect on the nature of its randomness and hence measuring a single series for the mean is the same as measuring many series that it produces. They are all the same so why worry? But many processes are not ergodic. For example, suppose we have two random number generators one producing numbers with a mean of 1 and the other a mean of -1. Suppose that which we get is equally likely when we switch the machine on. Now you can see that you no longer have an ergodic process. If you switch on and measure for a long time you will discover that the process has a mean of either 1 or -1 but if you switch on and off and measure many series you will find that the mean is zero (because you get -1 and +1 equally often). This is also the distinction that physicists make between measuring a quantity across all possible states and measuring it over time. The two give the same answer if all possible states appear in the evolution of the system with equal probability. For example, can you find out everything you need to know about humans by observing a single human for their lifetime or do you need to observe all humans? Humans are probably not ergodic. Mathematicians work quite hard to prove that a system is ergodic and a lot of very simple systems and quite complex ones aren't. If you know about Markov chains for example then a state is ergodic if it is aperiodic and non-absorbing. If all the states are ergodic then the chain is said to be ergodic and in this case you can assume that a statistic calculated from one realization of the chain is going to be a reasonable estimate of a statistic calculated from many realizations. Ergodic systems are ones that are in a sense thoroughly mixed and as such they have similarities to chaotic systems. Another of the things we can thank Sinai for is a game of billiards. If you bounce a billiard ball around a table forever is the system ergodic? The answer is usually no because there are usually periodic solutions. That is you can find an initial angle the makes the ball bounce along the same repeating path forever - imagine simply launching the ball at right angles to the cushion where it bounces back and forth along the same path forever. Clearly this is not typical and any statistics you compute from this piece of behaviour will not be typical of the entire behaviour of the system Sinai's game of billiards has a difference that makes it ergodic and it was one of the first dynamical systems to be proved ergodic. The difference is that in dynamical billiards there is a circular reflector in the middle of the table.
Credit:G. Stamatiou based on wikipedia user XaosBits
Now try and get a repeating bounce! This is an ergodic system and it is also chaotic - two slightly different starting configurations give two very different long term paths i.e. we have large sensitivity to initial conditions. The link between ergodic and chaotic is made even stronger in Sinai's next big contribution with Kolmogorov. Together they managed to generalize the concept of entropy to measure the unpredictability of dynamical systems. Kolmogorov-Sinai KS entropy is zero if a system is perfectly predictable and non-zero for systems that are increasingly unpredictable all the way up to chaotic systems. Later the connection between the KS entropy and the "classical" Lyapunov exponent was proved, with Pesin's theorem. Of course this is just an introduction, a flavour of the work that Sinai is responsible for. His name is associated with a number of new concepts and theorems and he has published over 250 papers. However, it seems more than likely that his work will have even more effect after being brought to the attention of the wider community.
More InformationRelated ArticlesConfronting The Unprovable - Gödel And All That What is a Turing Machine?Axiom Of Choice - The Programmer's Guide The Programmer's Guide To The Transfinite
To be informed about new articles on I Programmer, install the I Programmer Toolbar, subscribe to the RSS feed, follow us on, Twitter, Facebook, Google+ or Linkedin, or sign up for our weekly newsletter.
Comments
or email your comment to: comments@i-programmer.info |
|||
| Last Updated ( Wednesday, 14 April 2021 ) |