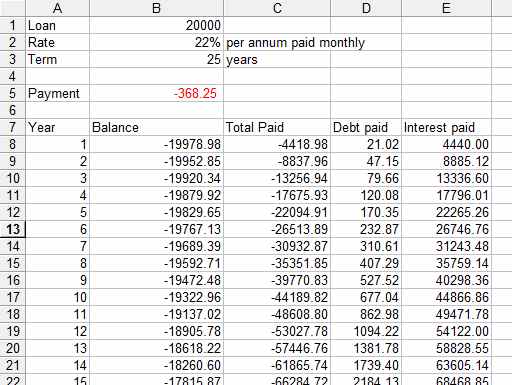
Loan schedule calculator

Using these formulas it is quite easy to put together a spreadsheet that will detail the state of a repayment loan at any stage in its life. The only real problem is allowing for the required number of months in the table.

First enter all of the text and Loan, Rate and Term data as shown in the screen dump.

Enter 1 in A8 to start the formula off and enter:

=FV($B$2/12,A8*12,$B$5, $B$1) in B8
=$B$5*A8*12 in C8
=$B$1+B8 in D8
=-(C8-D8) in E8

The first formula computes the state of the account at the end of each year. The second works out the total amount paid by the end of the year and the final two work out the amount of the debt paid off and the amount paid in interest to date.

Next fill column A with as many year numbers as you are interested in and copy the formulas in B8:G8 into the same number of rows.

You can see an example of a 25-year loan in the spreadsheet. Notice the way that the first year's payments only succeed in paying off $21.02 of the principal even though over $4400 is paid! Over the 25-year period of the loan more than $130,000 is paid in interest.

The basic loan spreadsheet

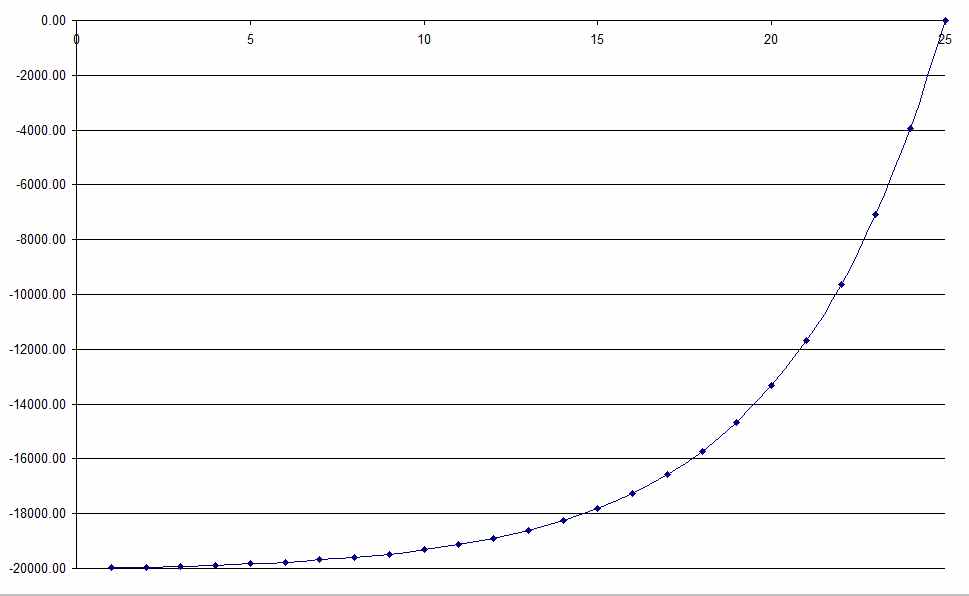
Loan balance reduction over time

The way in which loan repayments affect the amount you owe is much easier to appreciate in a chart which can be constructed directly from this spreadsheet with Year (Column A) on the x-axis and Balance (Column B) on the y-axis.

If you look at the graph of the balance against time you can see the characteristic shape of the repayment loan. The principal is paid off only slowly at first but the speed of repayment increases dramatically in the final years.

The rate of decrease of a repayment loan

Notice that there is no real decrease in the amount owed for the first 15 years. This is the reason why additional payments early in the life of a loan can greatly reduce the total cost. 

 Financial Functions

 Buy from Amazon

Spreadsheets take the hard work out of calculations, but you still need to know how to do them. Financial Functions with a spreadsheet is all about understanding and reasoning, using a spreadsheet to do the actual calculation.

1. Understanding Percentages
   Percentages are something familiar to us all - but they present many pitfalls that need to be avoided.
   
   
2. Interest Simple and Compound
   We explore the idea of borrowing money for a specified rate of interest or earning interest on an investment. The ideas of Present and Future Value PV and FV are introduced. 
   
   
3. Effective Interest Rates
   We explore the idea of the `effective’ annual interest rate and then on to the Effective Interest Rate/Annual Percentage Rate, the much quoted EIR or APR.
   
   
4. Introduction to Cashflow - Savings Plans
   In the first of three chapters covering the way in which interest rate affects cashflow we explore savings - but first we introduce some general ideas that apply equally to annuities and repayment loans.
   
   
5. Cashflow Continued - Annuities
   We move on to annuities in the second of three chapters devoted to exploring the way in which interest rate affects 
   
   
6. Exploring Repayment Loans
   Repayment loans are the subject of the last of three chapters which look at the effects of regular cashflows.
   
   

7. Present and Future Values
   The principles of present and future value apply even if the cash flow is irregular. The calculations are just a matter of breaking down the cash flow calculations into simple steps.
   
   

8. Investment Analysis
   How is it possible to evaluate investments that generate irregular cashflows? We explore how NPV can be used to make investment decisions.
   
   

9. Advanced Investment Analysis IRR and MIRR
   The IRR is perhaps the most complicated of the measures of the value of an investment with an irregular cash flow. Understanding exactly what it means is a good step toward making correct use of it. 
   
   

<ASIN:1871962013>

<ASIN:B07S79ZVMQ>

Comments

Make a Comment or View Existing Comments Using Disqus

or email your comment to: comments@i-programmer.info

<ASIN: 0470475366>

<ASIN:1118510100>

<ASIN:0735672431>

<ASIN:0789748576>

<ASIN:0470178892>

<ASIN:0195301501>

<ASIN:1119067510>