The effective percentage

Often a good way of summarizing a complex transaction which involves different payments and different percentages at different times is to compute a single effective percentage that would be applied to give the same output give the same inputs. The first example of this that we encounter is the use of repeated percentage discounts or charges on a single transaction. 

If you are offered a discount of P% and then a further discount of Q% on the discounted price, it is worthwhile asking what actual discount you are receiving on the original price? This sounds like a difficult question but it is very easy.

As the twice discounted price is given by:

price*(1-P)*(1-Q)

if the total actual discount percentage is D% then the final discounted price is:

price*(1-D)

and so:

price*(1-D)=price*(1-P)*(1-Q)

cancelling price from both sides gives the relationship between Q, P and D:

(1-D)=(1-P)*(1-Q)

Finally solving for D gives:

D=1-(1-P)*(1-Q)

or using the result we got earlier:

D = P + Q - P*Q

The same is true of percentage increase, but in this case the formula for the actual percentage increase is (1+P)*(1+Q)-1. That is, if a value is increased by P% and then the result further increased by Q%, the total percentage increase is:

D=(1+P)*(1+Q)-1

or:

D = P + Q + P*Q

Which version of the formula to use in any given case is up to you. 

For example, if a sales person offers you a further 5% discount on a price that has already been discounted by 10% the total discount is:

1-(1-0.1)*(1-0.05)

which works out to 14.5% as before. 

If you are initially charged 8% more for a holiday booking and then just before you leave a 15% fuel surcharge is added then the total percentage surcharge is (1+0.08)*(1+0.15)-1 or 24.2% increase on the original price.

This is the first and simplest example of an actual or effective percentage. Later when we look at percentages as interest rates we will meet the best known example of actual percentages, the APR or Actual Percentage Rate.

For now let’s look at another simpler, but practical, question concerning percentages and interest rates. 

Simple tax relief

If you take out a loan at I% interest what is the effective rate if the interest payments are subject to 25% tax relief?

In other words, what rate of interest would result in the same repayments without the tax relief?

We will ignore for the moment questions of repayment, what term the loan is for and the frequency of interest payments. So, if the loan is for M, the interest due each period is simply:

M*I

If the interest is tax free T% of it would otherwise have been paid to the tax authority and so does not represent an additional outgoing. This reduces the interest payment by T% and makes the effective interest paid only:

M*I*(1-T)

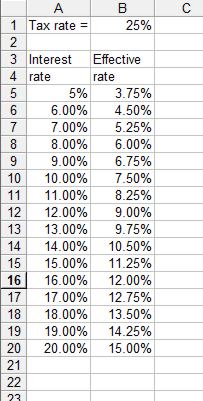
and so the effective rate of interest is I*(1-T)%, i.e. the rate is reduced by T%.

It is interesting to examine the way tax relief changes interest rates and so a simple spreadsheet is called for.

Starting from an empty spreadsheet enter the labels as shown in Figure 4 and the following formulas and values:

A5   5%
A6   =A5+0.01
B5   =A5*(1-$B$1)

Copy the formula in A6 into A7..A20 and the formula in B5 into B6..B20. Finally format B1 and A5..B20 as percentages.

Note: the use of $B$1 is an absolute cell reference that copying the formula will not alter it.

You can see a sample table in Figure 4 for a 25% rate of tax. You can, of course enter any tax rate you want to into cell B1.

Tax relief

Negative percentages

Although we could carry on dealing with percentage increase and decrease as separate cases, it is much simpler to adopt the convention that a positive percentage is an increase and a negative percentage a decrease. In this case to increase/decrease a value by P% you simply multiply by (1+P) and let the positive and negative signs take care of themselves. So remember from now on:

• a negative percentage corresponds to a percentage decrease and a positive percentage to a percentage increase and in either case we multiply by (1+P).

To see how this simplifies things you only have to look at the formula for the actual percentage which now becomes:

(1+P)*(1+Q)-1

or:

P + Q - P*Q

for both an increase and a decrease. However, you have to be careful about signs if you are doing the calculation in your head. 

Why do we use percentages?

The use of percentages in many financial situation is so natural that is is worth spending a few moments considering why this is so.

If you need to divide something up into portions so that each person gets an appropriate share of the whole then percentages are a good way to go about it.

If a pie is divided into two parts so that A gets twice as much as B then the appropriate percentages are 66.66...% and 33.33....%. As long as the pie is shared out into these percentages the two-to-one ratio will be maintained.

When relative importance is gauged as a ratio then a percentage allocation is appropriate. However notice that as the total amount to be divided increases the absolute gap between what A and B receive increases.

This property of a percentage increase/decrease of keeping ratios fixed is less arguably appropriate when what is being shared is less obvious.

For example, if A and B work for an hourly rate of $20 per hour and $10 per hour then a percentage wage rise of 10% will keep the two-to-one payment the same at $22 per hour and $11 per hour. However, the differential between the two rates of pay has jumped from $10 to $11. If a percentage increase is repeatedly applied the differential between the hourly rates goes on steadily rising even though the two-to-one ratio remains unchanged.

This isn’t necessarily wrong, but it is important that all concerned understand that a percentage increase or decrease keeps existing ratios fixed but changes absolute differences.

Key points

• A percentage is best entered and stored in a spreadsheet as a decimal fraction. In most spreadsheets this happens automatically if you enter a value followed by a % sign. You can also set a percentage display format to show decimal fractions as percent. That is, entering 33% stores 0.33 in a cell and setting the display format to percent makes it display as 33%.

• If a percentage is stored as a decimal fraction you can work out that percentage of another value simply by multiplying.
  
  
• To increase a quantity by I% multiply by (1+I)
  
  
• To decrease a quantity by I% multiply by (1-I)
  
  
• To recover a value that has been increased by I% divide by (1+I) and to recover a value that has been decreased by I% divide by (1-I)
  
  
• Finding P% of a quantity and then Q% of the result is not the same as finding (P+Q)% of the original value.
  
  
• In the same way increasing/decreasing a value by P% and then increasing/decreasing it by Q% is not the same as increasing/decreasing it by (P+Q)%.
  
  
• Using a negative percentage to mean a percentage decrease simplifies most formulas involving percentages.
  
  
• Percentage increases/decreases maintain existing ratios but change absolute differences in size.

 Financial Functions

 Buy from Amazon

Spreadsheets take the hard work out of calculations, but you still need to know how to do them. Financial Functions with a spreadsheet is all about understanding and reasoning, using a spreadsheet to do the actual calculation.

1. Understanding Percentages
   Percentages are something familiar to us all - but they present many pitfalls that need to be avoided.
   
   
2. Interest Simple and Compound
   We explore the idea of borrowing money for a specified rate of interest or earning interest on an investment. The ideas of Present and Future Value PV and FV are introduced. 
   
   
3. Effective Interest Rates
   We explore the idea of the `effective’ annual interest rate and then on to the Effective Interest Rate/Annual Percentage Rate, the much quoted EIR or APR.
   
   
4. Introduction to Cashflow - Savings Plans
   In the first of three chapters covering the way in which interest rate affects cashflow we explore savings - but first we introduce some general ideas that apply equally to annuities and repayment loans.
   
   
5. Cashflow Continued - Annuities
   We move on to annuities in the second of three chapters devoted to exploring the way in which interest rate affects 
   
   
6. Exploring Repayment Loans
   Repayment loans are the subject of the last of three chapters which look at the effects of regular cashflows.
   
   

7. Present and Future Values
   The principles of present and future value apply even if the cash flow is irregular. The calculations are just a matter of breaking down the cash flow calculations into simple steps.
   
   

8. Investment Analysis
   How is it possible to evaluate investments that generate irregular cashflows? We explore how NPV can be used to make investment decisions.
   
   

9. Advanced Investment Analysis IRR and MIRR
   The IRR is perhaps the most complicated of the measures of the value of an investment with an irregular cash flow. Understanding exactly what it means is a good step toward making correct use of it. 
   
   

<ASIN:1871962013>

<ASIN:B07S79ZVMQ>

Comments

Make a Comment or View Existing Comments Using Disqus

or email your comment to: comments@i-programmer.info

<ASIN:/0230348114>

<ASIN:1118510100>

<ASIN:0735672431>

<ASIN:1118558766> 

<ASIN:1118656210>

<ASIN: 047027560X>