| The Lost Art Of The Storage Mapping Function |
| Written by Harry Fairhead | ||||
| Thursday, 04 October 2018 | ||||
Page 2 of 3
Key Mapping and TreesThe two-dimensional array SMF is beginning to look a little more interesting but it still nothing more than an application of the idea of using a function f(key) to locate the data corresponding a key. In the case of the one-dimensional array the key is simply the index i and the location of a[i] is given by f(i) and in the two-dimensional case the keys are i and j and the location of a[i,j] is given by f(i,j). Higher dimensional arrays can be treated in the same way. At this point my guess is that many a high-level language programmer will be thinking how could an SMF be at all useful to me? After all, high-level languages keep programmers well away from real memory locations. The answer is that while most languages provide simple data structures such as arrays, they often don't provide the rarer data structures such as trees. Even when they do there are times when an SMF implementation of a simple or exotic data structure can be useful. The trick is to use an array as if it was a chunk of old-fashioned linear memory and a suitable SMF to map the new data structure onto the array. Puzzled? Well let's try a simple binary tree implementation. A binary tree is a tree structure such that each node, apart from the final or terminal nodes, has exactly two children - hence the binary in binary tree. Each node is associated with a value that takes n bytes to store then a suitable SMF is:
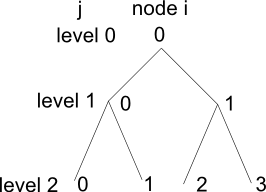
which gives the location of the value stored at ith node at the jth level. That is we are using i and j to "index" the tree by node number i at level j. To see why this works consider the following small binary tree:
and so on. Notice that going from one level to the next doubles the number of nodes and you should be able to work out that the number of nodes at level j is simply 2j. With this insight you should now also be able to see how the SMF works. The tree is stored as lines of nodes one level at a time. That is:
To make use of this SMF in a high-level language all you have to do is declare an array of elements that will hold the node values and use the SMF with n=1 to determine which element node i at level j is stored in. For example, if the array is a[N] then node i at level j is stored in a[i+2^j-1]. You can see the general idea. If you have a data structure which has a regular pattern then you need to find a function that maps the regular pattern to a linear sequence of storage locations. Basically you need a function which enumerates the elements of the data structure one after another. Inventing a storage mapping function can be tricky but its always possible - unless the data structure can't be enumerated. A Practical Application - A Database ArrayIf binary trees sound too unlikely to gain your interest in SMFs then perhaps it is worth pointing out their use with respect to disk files. For example, suppose you need a 2D array bigger than RAM will allow then as long as you have a fast hard disk available what could be easier than implementing a virtual array using a random access file or a database table. Simply set up a random access file such that each record can hold exactly one value and then when you want to access the value of a[i,j] seek record number i + n*j where n is the size of the first dimension. You can probably work out for yourself various ways of making the process more efficient - for example by defining a record large enough to hold a complete row of the array etc. The same principles apply to creating any virtual data structure on disk - store each element of the data structure in a record and use an SMF to find which record corresponds to each element. It is also worth pointing out that this is how databases are implemented. In this case you set up a file of a given size and consider it to consist of fixed size records. If each record uses b Bytes of storage then the location of the ith record is obviously:
and this is were you perform a random access seek to and read in b bytes to get the ith record. In many cases you don't lookup the database using the record number but a more general key. In this case there is an extra step - lookup the record number you need in a key table. In other words, if you want to find the record containing the data corresponding to "key" you first look "key" up in the index which gives the record number. This works in all cases unless the record size is variable when you need a different approach. |
||||
| Last Updated ( Thursday, 04 October 2018 ) |