| From Data To Objects |
| Written by Alex Armstrong | ||||
| Thursday, 03 January 2019 | ||||
Page 2 of 3
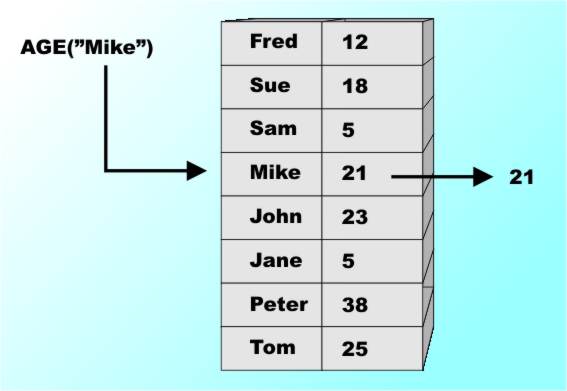
The Limits Of ImplementationAt this point many accounts of data start to explain exactly how data is stored in a machine. This is important because how it works affects how quickly it works and how much memory you need to implement it. For example an AGE array designed to store 50 million ages would need something like 100Mbytes of storage to store a 2-digit age for everyone. Now while this sort of information is essential to building practical working systems it could be argued that efficiency is something for the hardware and compiler people to sort out. This is a philosophical turn of mind – are we being pure or practical? For example, once you have invented the simple array you might well go on to invent something that you deem to be a small extension but most programmers have been taught to consider as something completely different. If you can use an index like 3 or 7 or 8 why not use an index like 3.5 or 6.7 or “john” or anything really. Why not use an array that will store peoples ages so that they can be looked up by name e.g. AGE(“john doe”)? The answer is that you can but the difficulty of implementing such an array causes programmers to think of it as something different. Such an array is usually called a “collection”, a “dictionary” or an “associative array”. The distinction isn't really a theoretical one because the notion of the basic look up A("john doe") is exactly the same as A(10) - i.e. retrieve the data stored under the supplied key or index. The difference is that the index can be used directly to retrieve the data value by doing a computation that gives the required element. For example if you know that the array A starts at memory location 1000 and each element uses 4 bytes then you will find A(10) at location 1000+4*10. The whole point is that given the index you can go directly to the element with only a little arithmetic. The problem of looking up the element corresponding to "john doe" is clearly not the same. So we have a problem of implementing a more advanced form of array but there is also the issue that the more advanced form has different properties and this means it really should be treated as something special in its own right. The Dictionary or Associative ArrayThe basic idea of using a non-integer "index" is the same as an array but there are some important differences that might just be important enough to merit the change of name. The first obvious difference is that you can’t “step through” an associative array. For example, to see all of A(I) then you simply set I to 1, 2, 3 and so on to 10. To see all of AGE(name) you haven’t a clue as to how to vary name in an obvious or natural sequence to go though everyone. There also isn’t an obvious first or last element in AGE and there isn’t even an obvious “next” or “previous” element in general. These are the real reasons for considering an associative array to be something different and new – not just the difficulty of actually implementing it! So how would you implement an associative array? Well the simplest way would be to use two standard arrays – store the name in one and the age in the other at the same index value you stored the name. Now when you want to look up an age you have to scan through the NAME array until you find the name, stored at index I say and then you lookup the age stored in the age array as AGE(I). You can see that this isn’t very efficient as soon as you consider searching through 60 million names in random order. You can improve the search time by keeping the array of names in alphabetical order but now you are really getting complicated because you have to sort the arrays and keep them in order if a new name has to be added or deleted! It is easy to see that this gets very complicated very quickly and hence most programming languages don’t offer associative arrays as a fundamental language facility. However many of the newer languages Python, JavaScript, Ruby and Perl do make it a core feature. The reason is that a good way of implementing the associative array was worked out.
An associative array – look up in one array, return the answer from the second The Storage Mapping FunctionThe reason that the indexed array is easy to implement is that you can take the index and use it to compute the location of the element you are looking for. That is there is a function, the Storage Mapping Function, F which when given the index returns the memory location that the array element is stored in. That is if you want A(34) then it is stored in memory location F(34). For an array the SMF is simple:
where size is the amount of memory each element takes to store. In the early days of computing only data structures which had a simple SMF were built into languages because these were the only ones we had the know how to implement. As things developed it was realized that you could use an SMF in the form of a hash function to create more complex data structures and the associative array in particular. A hash function is a function that converts a key into a numeric value. Ideally a hash function should convert each key into a different numeric value but there are ways of living with situations where different keys are mapped to the same value - as long as it doesn't happen too often. So suppose we have a hash function that converts strings to numbers now we can create an SMF something like:
It now looks exactly like the way we implement an index array and it is fast and reasonably efficient. Of course finding good hash functions isn't easy and there are lots of details of implementation but once we mastered the hash based SMF we could have associative arrays. Today there is even criticism of languages that supply associative arrays as a primitive data type and particularly of languages that make it their fundamental data type. It has become so easy to implement associative arrays that they are now the core of many dynamic languages and it is claimed they are responsible for a slow and sluggish performance and they make it difficult to speed the language implementations up. However - associative arrays make programming much easier. <ASIN: 0130224189> <ASIN:0672324539> <ASIN:0201000237> |
||||
| Last Updated ( Thursday, 03 January 2019 ) |