| Binary Arithmetic |
| Written by Mike James | |||||||
| Monday, 30 October 2023 | |||||||
Page 3 of 3
Logic and switchesAfter George Boole had described his Boolean logic, and after various people had built logical machines based on it, the simplicity of the “true/false” algebra was beginning to be understood. Charles Pierce sketched out how batteries and switches could be used to calculate logic but this was ahead of its time. Fifty years later in the 1940 Claude Shannon looked at the ideas again and noticed that he could build not just logic circuits using high and low voltages to represent true and false, he could also build arithmetic circuits. All you have to do is write down the addition table for binary arithmetic for a single “digit” or bit:
You might recognise this as the truth table for the Exclusive OR and this is indeed all that is needed to add two bits together - as long as you are prepared to ignore the carry. In other words the addition table for binary symbols is the same as the Exclusive OR in logic. If you want to generate the carry then you need to add another column to the logic table
Now you can see that the carry is simply an And operation. Looking back at the addition table for binary you can now see that it can be represented using nothing but an Exclusive OR and an And gate. Put the two together and you can add two bits and generate a result and a carry - this is called a half adder because it doesn’t deal with the problem of taking account of anything that might have been generated by an earlier pair of bits being added.
To create a full adder all we need to do is combine two half adders so that the first adds the two bits to produce a result and a carry and the second adds the result and the carry to produce a final result and a final carry.
A full adder takes two bits and the carry from the previous addition and produces a result and a carry
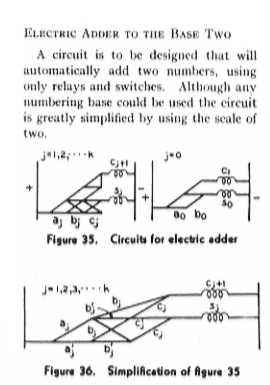
A little while after Shannon worked out that binary arithmetic was very easy to implement, the same idea was rediscovered by George Stibitz. He was musing on the problems of using relays in telephone circuits when he suddenly realised that he could use the open/closed positions as 0/1 and do arithmetic. He quickly worked out a half adder and built it on his kitchen table using light bulbs to show the results. In 1940 he demonstrated a simple binary relay computer and in the audience was John Mauchly who went on to build, with John Eckert, the first electronic computer - ENIAC.
Shannon and his first adder
Decimal Not Yet Dead!The big shock is that ENIAC, one of the first electronic computers, was a decimal computer not a binary computer. Part of the reason was that the electro-mechanical computers that came before it were decimal but it must also have been that the advantages of binary just weren’t that obvious - even though this seems incredible. The only exception to the rule that early computers were decimal was Conrad Zuse’s Z1 built in 1936. It also seems that he realised that binary was the way to build a computer in 1935, which gives him a strong claim to have thought of the idea before Shannon or Stibitz. Switching to binary was such a simplification that Zuse was able to build complete computers on his kitchen table. Representing numbers in binary makes the connection not only with electro-mechanical switching circuits but with more advanced electronics. Once you settle on using binary it becomes very easy to find physical systems that have two states that can be used to represent 0 and 1. This makes creating storage and memory devices very simple. You can use everything from holes punched in paper tape or cards to the direction of magnetisation to represent numbers in binary. However, there is a cost-efficiency. If you code a number using binary then each storage location stores a single bit but if you can find a way to store more than just two states at a particular location then you can store more data in the same space. Put another way, a binary number has more bits in it than the equivalent decimal number has digits. For example, the decimal number 1234 is 10011010010 in binary. Binary numbers take more space and we trade space for simplicity. Some forms of Flash memory, for example, use three or more voltage levels to store data using non-binary bases. So far no one has gone back to basics to build a decimal computer but one day, when binary computers have run out of steam, perhaps Babbage will be proved right. For more on binary numbers and two's complement representation in particular, see Binary - negative numbers
Related Articles
What Programmers Know
Contents
* Recently revised
Comments
or email your comment to: comments@i-programmer.info To be informed about new articles on I Programmer, sign up for our weekly newsletter, subscribe to the RSS feed and follow us on Twitter, Facebook or Linkedin.
<ASIN:0521370957> <ASIN:0763741493> <ASIN:0596510047> <ASIN:0060512806>
|
|||||||
| Last Updated ( Saturday, 04 November 2023 ) |
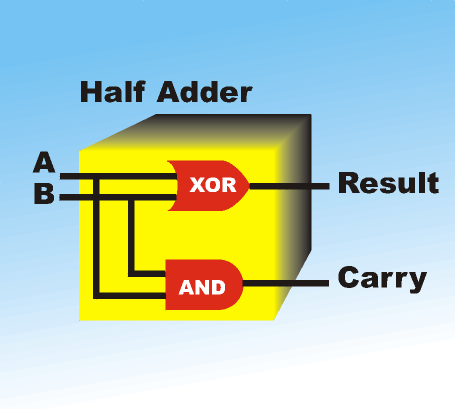 A half adder takes two bits and adds them to give a result and a carry
A half adder takes two bits and adds them to give a result and a carry