| Non-Computable And Other Numbers |
| Written by Mike James | ||||||
| Thursday, 14 March 2019 | ||||||
Page 2 of 5
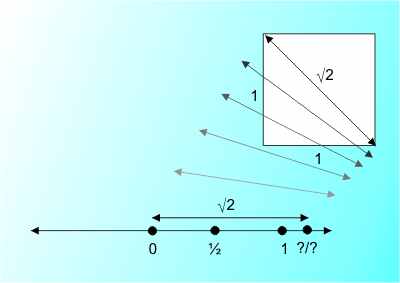
You don't need to know the proof to trust its results but the proof is very simple but skip this section if you want to. Suppose that you can express the square root of 2 as a rational number in its lowest terms i.e. all factors cancelled out, as a/b. Then (a/b)2 is 2 by definition and hence a2=2b2. This implies that a2 is even and hence a has to be even (as odd numbers squared are still odd). Suppose a=2c for some integer c. Thus b=2d for some integer d. Now we can write a/b=2c/2d which means that a/b isn't in its lowest form as we can now remove a factor of 2 to get c/d. As you can reduce any fraction to its lowest form by cancelling common factors there can be no a/b that squares to give 2.
You can show that a line square root of two long exists and so there has to be a point on the number line that is that far from zero. Is there a rational number corresponding to this point? The simple answer is no! What this means is that if we only have the integers and the fractions or the rationals (because they are a ratio of two integers) then there are points on the line that do not correspond to a number - and this is unacceptable. The solution is that we simply expanded what we regard as a number and the irrational numbers were added to the mix. But what exactly are irrationals and how can you write one down? This is a question that occupied mathematicians for a long time and it took a while to get it right. Today we think of an irrational number as a value with an infinite sequence of digits after the decimal point. This sequence of digits goes on forever and can never fall into a repeating pattern because if it does it is fairly easy to show that the value is a rational. That is in decimal 0.33333333333333 repeating for ever isn't an irrational number because it repeats and it is exactly 1/3 i.e. it is rational. Notice that there is already something strange going on because while we have an intellectual solution to what an irrational is we still can't write one down. How could you as the digits never end and never fall into a repeating pattern. This means that in general writing an irrational down isn't going to be a practical proposition. And yet I can write down √2 and this seems to specify the number precisely. Also what sort of equations do irrationals solve? A partial answer is that they are solutions to equations like an=x and more generally they are solutions to polynomial equations. The problem is that only a relatively small proportion of the irrationals come from the roots of polynomials as we shall see. Now we have integers like one or minus two, fractions like 5/6 and irrationals like the square root of two. From the point of view of computing this is where it all gets very messy. EnumerationsTo see this you only have to think a little about iteration or enumeration. Put simply anything you can count out is enumerable. Integers are enumerable - just write a for loop.
which enumerates the integers 0 to 10. Even an infinite number of integers are enumerable its just the for loop would take a little while longer to complete!
Ok, the loop would never end but if you wait long enough you will see every integer displayed. In this sense, the integers, all of them, are enumerable. The point is that for any particular integer that you can specify the wait is finite. Now the next question is are the rationals enumerable? The answer at first look seems to be no because of the following little problem. Suppose you start your for loop at zero. The next integer is one but what is the next rational? The answer is that there isn't one. You can get as close as you like to zero by making the fraction smaller and smaller 1/10. 1/100, 1/1000 and so on. There is no next fraction (technically the fractions are "dense") and this seems to make writing a for loop to list them impossible. However this isn't quite the point. We don't need to enumerate the fractions in any particular order we just need to make sure that as long as the loop keeps going every rational number will eventually be constructed. So what about:
You should be able to see that if you wait long enough every fraction will eventually be displayed. In fact we are generating each fraction an infinite number of times because of identical terms like 1/2, 2/4. 4/8 and so on.. We can agree that even an infinite set is enumerable as long as you are guaranteed to see every element if you wait long enough.
<ASIN:0521430690> <ASIN:9810230818> <ASIN:0285635948> <ASIN:0691024472> |
||||||
| Last Updated ( Saturday, 16 March 2019 ) |